江苏省淮安市2018年中考数学试卷

试卷更新日期：2018-07-10 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣3的相反数是（）。

A、﹣3 B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看试题解析
2. 地球与太阳的平均距离大约为150 000 000km，将150 000 000用科学记数法表示应为（）。

A、15×10⁷ B、1.5×10⁸ C、1.5×10⁹ D、0.15×10⁹

查看试题解析
3. 若一组数据3、4、5、x、6、7的平均数是5，则x的值是（）。

A、4 B、5 C、6 D、7

查看试题解析
4. 若点A(﹣2，3)在反比例函数 $y = \frac{k}{x}$ 的图像上，则k的值是（）。

A、﹣6 B、﹣2 C、2 D、6

查看试题解析
5. 如图，三角板的直角顶点落在矩形纸片的一边上，若∠1＝35°，则∠2的度数是（）。

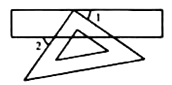A、35° B、45° C、55° D、65°

查看试题解析
6. 如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（）。

A、20 B、24 C、40 D、48

查看试题解析
7. 若关于x的一元二次方程x²﹣2x﹣k＋1＝0有两个相等的实数根，则k的值是（）。

A、﹣1 B、0 C、1 D、2

查看试题解析
8. 如图，点A，B，C都在⊙O上，若∠AOC＝140°，则∠B的度数是（）。

A、70° B、80° C、110° D、140°

查看试题解析

二、填空题

9. 计算： ${(a^{2})}^{3}$ ＝．

查看试题解析
10. 一元二次方程x²﹣x＝0的根是．

查看试题解析
11. 某射手在相同条件下进行射击训练，结果如下：
射击次数n
10
20
40
50
100
200
500
1000
击中靶心的频数m
8
19
37
45
89
181
449
901
击中靶心的频率 $\frac{m}{n}$
0.900
0.950
0.925
0.900
0.890
0.905
0.898
0.901

该射手击中靶心的概率的估计值是（明确到0.01）．

查看试题解析
12. 若关于x ， y的二元一次方程3x﹣ay＝1有一个解是 ${\begin{cases} x = 3 \\ y = 2 \end{cases}$ ，则a＝．

查看试题解析
13. 若一个等腰三角形的顶角等于50°，则它的底角等于．

查看试题解析
14. 将二次函数 $y = x^{2} - 1$ 的图像向上平移3个单位长度，得到的图像所对应的函数表达式是．

查看试题解析
15. 如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝5，分别以点A、B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧交点分别为点P、Q，过P、Q两点作直线交BC于点D，则CD的长是．

查看试题解析
16. 如图，在平面直角坐标系中，直线l为正比例函数y＝x的图像，点A₁的坐标为(1，0)，过点A₁作x轴的垂线交直线l于点D₁ ，以A₁D₁为边作正方形A₁B₁C₁D₁；过点C₁作直线l的垂线，垂足为A₂ ，交x轴于点B₂ ，以A₂B₂为边作正方形A₂B₂C₂D₂；过点C₂作x轴的垂线，垂足为A₃ ，交直线l于点D₃ ，以A₃D₃为边作正方形A₃B₃C₃D₃；…；按此规律操作下去，所得到的正方形A_nB_nC_nD_n的面积是．

查看试题解析

三、解答题

17.

(1)、计算： $2 \sin 45 ° + {(π - 1)}^{0} - \sqrt{18} + | - 2 \sqrt{2} |$ ；

(2)、解不等式组： ${\begin{cases} 3 x - 5 < x + 1 \\ 2 x - 1 \geq \frac{3 x - 1}{2} \end{cases}$ ．

查看试题解析
18. 先化简，再求值： $(1 - \frac{1}{a + 1}) \div \frac{2 a}{a^{2} - 1}$ ，其中a＝﹣3．

查看试题解析
19. 已知：如图，▱ABCD的对角线AC、BD相交于点O，过点O的直线分别与AD、BC相交于点E、F，求证：AE＝CF．

查看试题解析
20. 某学校为了解学生上学的交通方式，现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查，规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项，并将统计结果绘制了如下两幅不完整的统计图．

请解答下列问题：

(1)、在这次调查中，该学校一共抽样调查了名学生；

(2)、补全条形统计图；

(3)、若该学校共有1500名学生，试估计该学校学生中选择“步行”方式的人数．

查看试题解析
21. 一只不透明袋子中装有三只大小、质地都相同的小球，球面上分别标有数字1、﹣2、3，搅匀后先从中任意摸出一个小球（不放回），记下数字作为点A的横坐标，再从余下的两个小球中任意摸出一个小球，记下数字作为点A的纵坐标．

(1)、用画树状图或列表等方法列出所有可能出现的结果；

(2)、求点A落在第四象限的概率．

查看试题解析
22. 如图，在平面直角坐标系中，一次函数y＝kx＋b的图像经过点A(﹣2，6)，且与x轴相交于点B，与正比例函数y＝3x的图像交于点C，点C的横坐标为1．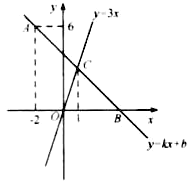

(1)、求k、b的值；

(2)、若点D在y轴负半轴上，且满足S_△_COD＝ $\frac{1}{3}$ S_△_BOC ，求点D的坐标．

查看试题解析
23. 为了计算湖中小岛上凉亭P到岸边公路l的距离，某数学兴趣小组在公路l上的点A处，测得凉亭P在北偏东60°的方向上；从A处向正东方向行走200米，到达公路l上的点B处，再次测得凉亭P在北偏东45°的方向上，如图所示．求凉亭P到公路l的距离．（结果保留整数，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
24. 如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．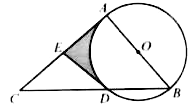

(1)、试判断直线DE与⊙O的位置关系，并说明理由；

(2)、若⊙O的半径为2，∠B＝50°，AC＝4.8，求图中阴影部分的面积．

查看试题解析
25. 某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件．

(1)、当每件的销售价为52元时，该纪念品每天的销售数量为件；

(2)、当每件的销售价x为多少时，销售该纪念品每天获得的利润y最大？并求出最大利润．

查看试题解析
26. 如果三角形的两个内角 $α$ 与 $β$ 满足 $2 α + β$ ＝90°，那么我们称这样的三角形为“准互余三角形”．

(1)、若△ABC是“准互余三角形”，∠C＞90°，∠A＝60°，则∠B＝°；

(2)、如图①，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝5，若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．

(3)、如图②，在四边形ABCD中，AB＝7，CD＝12，BD⊥CD，∠ABD＝2∠BCD，且△ABC是“准互余三角形”．求对角线AC的长．

查看试题解析
27. 如图，在平面直角坐标系中，一次函数 $y = - \frac{2}{3} x + 4$ 的图像与x轴和y轴分别相交于A、B两点．动点P从点A出发，在线段AO上以每秒3个单位长度的速度向点O作匀速运动，到达点O停止运动．点A关于点P的对称点为点Q，以线段PQ为边向上作正方形PQMN．设运动时间为t秒．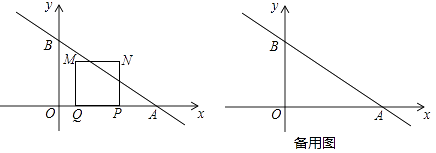

(1)、当t＝ $\frac{1}{3}$ 秒时，点Q的坐标是；

(2)、在运动过程中，设正方形PQMN与△AOB重叠部分的面积为S，求S与t的函数表达式；

(3)、若正方形PQMN对角线的交点为T，请直接写出在运动过程中OT＋PT的最小值．

查看试题解析

射击次数n	10	20	40	50	100	200	500	1000
击中靶心的频数m	8	19	37	45	89	181	449	901
击中靶心的频率 $\frac{m}{n}$	0.900	0.950	0.925	0.900	0.890	0.905	0.898	0.901