北京四中2017-2018学年高一下学期数学期中考试试卷

试卷更新日期：2018-07-09 类型：期中考试

进入出卷网下载

一、单选题

1. 某影院有40排，每排46个座位，一次新片发布会坐满了记者，会后留下了每排20号的记者进行座谈，这样的抽样方法是（）

A、抽签法 B、随机数表法 C、系统抽样法 D、分层抽样法

查看试题解析
2. 下列命题中，正确命题的个数是（）
①有三个公共点的两个平面重合 ②梯形的四个顶点在同一平面内
③三条互相平行的直线必共面 ④四条线段顺次首尾相接，构成平面图形

A、0 B、1 C、2 D、3

查看试题解析
3. 如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，在正方形内随机取一点，则此点取自黑色部分的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{π}{8}$ C、 $\frac{1}{2}$ D、 $\frac{π}{4}$

查看试题解析
4. △ABC中，若B＝45°， $b = \frac{4}{3} \sqrt{3} ， c = 2 \sqrt{2}$ ，则A＝（）

A、15° B、75° C、75°或105° D、15°或75°

查看试题解析
5. 甲、乙两人掷骰子，若甲掷出的点数记为a，乙掷出的点数记为b，则｜a－b｜≤1的概率为（）

A、 $\frac{4}{9}$ B、 $\frac{7}{18}$ C、 $\frac{2}{9}$ D、 $\frac{1}{9}$

查看试题解析
6. 若a，b是异面直线，则与a，b都平行的平面（）

A、不存在 B、有无穷多个 C、有且仅有一个 D、不一定存在

查看试题解析
7. △ABC中，若∠ABC＝ $\frac{π}{4}$ ， $A B = \sqrt{2} ， B C = 3$ ，则sin∠BAC＝（）

A、 $\frac{\sqrt{10}}{10}$ B、 $\frac{\sqrt{10}}{5}$ C、 $\frac{3 \sqrt{10}}{10}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
8. 有5个大小相同的球，上面分别标有1，2，3，4，5，现任取两个球，两个球序号相邻的概率是（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{3}{10}$

查看试题解析
9. 为了了解高一年级学生的体锻情况，学校随机抽查了该年级20个同学，调查他们平均每天在课外从事体育锻炼的时间(分钟)，根据所得数据的茎叶图，以5为组距将数据分为八组，分别是[0，5)，[5，10)，…[35，40]，作出的频率分布直方图如图所示，则原始的茎叶图可能是（）

A、 B、 C、 D、

查看试题解析
10. 台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，B城市处于危险区内的时间为（）

A、0.5小时 B、1小时 C、1.5小时 D、2小时

查看试题解析
11. △ABC中，给出以下条件，有唯一解的是（）

A、 $a = 4 ， b = 5$ ，A＝30° B、 $a = 5 ， b = 4$ ，A＝60° C、 $a = \sqrt{3} ， b = \sqrt{2}$ ，B＝120° D、. $a = \sqrt{3} ， b = \sqrt{6}$ ，A＝60°

查看试题解析
12. 同时投掷两枚骰子，计算向上的点数之和，则以下各数出现概率最大的是（）

A、5 B、6 C、7 D、8

查看试题解析
13. 某科研小组有20个不同的科研项目，每年至少完成一项。有下列两种完成所有科研项目的计划：A计划：第一年完成5项，从第一年开始，每年完成的项目不得少于次年，直到全部完成为止；B计划：第一年完成项数不限，从第一年开始，每年完成的项目不得少于次年，恰好5年完成所有项目。那么，按照A计划和B计划所安排的科研项目不同完成顺序的方案数量（）

A、按照A计划完成的方案数量多 B、按照B计划完成的方案数量多 C、按照两个计划完成的方案数量一样多 D、无法判断哪一种计划的方案数量多

查看试题解析

二、填空题

14. 某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种，现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是.

查看试题解析
15. 甲、乙、丙三名射箭运动员在某次测试中各射箭20次，三人的测试成绩如下表，s₁、s₂、s₃分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则s₁、s₂、s₃的大小关系是.
甲的成绩
乙的成绩
丙的成绩
环数
7
8
9
10
环数
7
8
9
10
环数
7
8
9
10
频数
5
5
5
5
频数
6
4
4
6
频数
4
6
6
4

查看试题解析
16. △ABC中，若 $b = c ， a^{2} = 2 b^{2} (1 - sin A)$ ，则A＝。

查看试题解析
17. 集合 $A = {y | y = 6 n - 4 ， n = 1 ， 2 ， 3 ， 4 ， 5 ， 6}$ ，集合 $B = {y | y = 2^{n - 1} ， n = 1 ， 2 ， 3 ， 4 ， 5 ， 6}$ ，若任意A∪B中的元素a，则 $a \in$ A∩B的概率是。

查看试题解析
18. △ABC的三边长分别为4、5、6，若将三边都减少x后构成一个钝角三角形，则实数x的取值范围是。

查看试题解析
19. 下列四个命题：
①样本方差反映的是所有样本数据与样本平均值的偏离程度；②基本事件空间是Ω＝{1，2，3，4，5，6}，若事件A＝{1，3}，B＝{3，5，6}，A，B为互斥事件，但不是对立事件；③某校高三（1）班和高三（2）班的人数分别是m，n，若一模考试数学平均分分别是a，b，则这两个班的数学平均分为 $\frac{n a}{m} + \frac{m b}{n}$ ；④如果平面外的一条直线上有两个点到这个平面的距离相等，那么这条直线与这个平面的位置关系为平行或相交。
其中真命题的序号是。

查看试题解析
20. 变量X与Y相对应的5组数据和变量U与V相对应的5组数据统计如下表：
X
10
11.3
11.8
12.5
13

U
10
11.3
11.8
12.5
13
Y
1
2
3
4
5

V
5
4
3
2
1
用b₁表示变量Y与X之间的回归系数，b₂表示变量V与U之间的回归系数，则b₁与b₂的大小关系是。

查看试题解析
21. 从 $n$ 个正整数 $1 ， 2 ， \dots ， n$ 中任意取出两个不同的数，若取出的两数之和等于 $5$ 的概率为 $\frac{1}{14}$ ，则 $n =$ 。

查看试题解析
22. 已知 $n \in N^{*}$ ，则以3，5，n为边长的钝角三角形的个数是。

查看试题解析

三、解答题

23. 已知：正方体ABCD－A₁B₁C₁D₁ ，如图，

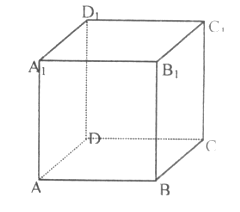
（Ⅰ）若E、F为AA₁、CC₁的中点，画出过D₁、E、F的截面；
（Ⅱ）若M、N、P为A₁B₁、BB₁、B₁C₁上的点（均不与B1重合），求证：△MNP是锐角三角形。

查看试题解析
24. 手机完全充满电量，在开机不使用的状态下，电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间。
为了解A，B两个不同型号手机的待机时间，现从某卖场库存手机中随机抽取A，B两个型号的手机各5台，在相同条件下进行测试，统计结果如下：
手机编号
1
2
3
4
5
A型待机时间（h）
120
125
122
124
124
B型待机时间（h）
118
123
127
120
a
已知A，B两个型号被测试手机待机时间的平均值相等。
（Ⅰ）求a的值；
（Ⅱ）求A型号被测试手机待机时间方差和标准差的大小；
（Ⅲ）从被测试的手机中随机抽取A，B型号手机各1台，求至少有1台的待机时间超过122小时的概率。
（注：n个数据 $x_{1} ， x_{2} ，$ … $， x_{n}$ 的方差 $s^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} +$ … $+ {(x_{n} - \bar{x})}^{2}]$ ，其中 $\bar{x}$ 为数据 $x_{1} ， x_{2} ，$ … $， x_{n}$ 的平均数）

查看试题解析
25. 已知：△ABC中，三边 $a ， b ， c$ 的对角为A，B，C，且 $\frac{cos C}{cos B} = \frac{3 a - c}{b}$ ，
（Ⅰ）求 $sin B$ 的值；
（Ⅱ）若 $b = 4 \sqrt{2}$ ，且 $a = c$ ，求△ABC的面积。

查看试题解析
26. 某人隔河看到两目标A与B，但都不能到达，该人在此岸选取相距 $\sqrt{3}$ 公里的C，D两点，测得∠ACB＝75°，∠BCD＝45°，∠ADC＝30°，∠ADB＝45°，如果A，B，C，D共面，求A与B的距离。

查看试题解析
27. 袋中有a个黑球和b个白球，随机地每次从中取出一球，每次取后不放回，记事件A为“直到第k次才取到黑球”，其中1≤k≤b；事件B为“第7次取出的球恰好是黑球”，其中1≤k≤b。
（Ⅰ）若a＝5，b＝3，k＝2，求事件A发生的概率；
（Ⅱ）判断事件B发生的概率是否随k取值的变化而变化？并说明理由；
（Ⅲ）比较a＝5，b＝9时事件A发生的概率与a＝5，b＝10时事件A发生的概率的大小，并说明理由。

查看试题解析

甲的成绩					乙的成绩					丙的成绩
环数	7	8	9	10	环数	7	8	9	10	环数	7	8	9	10
频数	5	5	5	5	频数	6	4	4	6	频数	4	6	6	4

手机编号	1	2	3	4	5
A型待机时间（h）	120	125	122	124	124
B型待机时间（h）	118	123	127	120	a

X	10	11.3	11.8	12.5	13		U	10	11.3	11.8	12.5	13
Y	1	2	3	4	5		V	5	4	3	2	1