2016-2017学年山东省日照市莒县九年级上学期期中数学试卷

试卷更新日期：2017-01-20 类型：期中考试

进入出卷网下载

一、选择题

1. 下列命题错误的是（）

A、等弧对等弦 B、三角形一定有外接圆和内切圆 C、平分弦的直径垂直于弦 D、经过切点且垂直于切线的直线必经过圆心

查看试题解析
2. 关于概率，下列说法正确的是（）

A、莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨 B、随机抛掷一枚质地均匀的硬币，落地后一定反面向上 C、在一次抽奖活动中，中奖的概率是1%，则抽奖100次就一定会中奖 D、同时抛掷两枚质地均匀硬币，“一枚硬币正面向上，一枚硬币反面向上”的概率是 $\frac{1}{2}$

查看试题解析
3. 若A（3，y₁），B（﹣2，y₂），C（﹣1，y₃）三点都在函数y=﹣ $\frac{1}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₁＞y₂＞y₃ C、y₁=y₂=y₃ D、y₁＜y₃＜y₂

查看试题解析
4. 如图，在⊙O中，AC∥OB，∠BAO=25°，则∠BOC的度数为（）

A、25° B、50° C、60° D、80°

查看试题解析
5. 在△ABC中，∠C=90°，AC=BC=4cm，D是AB的中点，以C为圆心，4cm长为半径作圆，则A，B，C，D四点中，在圆内的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，2.5cm为半径的圆与AB的位置关系是（）

A、相离 B、相交 C、相切 D、无法确定

查看试题解析
7. 如图，已知一块圆心角为270°的扇形铁皮，用它作一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是（）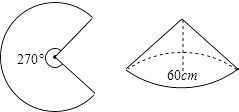

A、40cm B、50cm C、60cm D、80cm

查看试题解析
8. 正比例函数y₁=k₁x（k₁＞0）与反比例函数y₂= $\frac{k_{2}}{x}$ （k₂＞0）部分图象如图所示，则不等式k₁x＞ $\frac{k_{2}}{x}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
9. 某科研小组为了考查某河流野生鱼的数量，从中捕捞200条，作上标记后，放回河里，经过一段时间，再从中捕捞300条，发现有标记的鱼有15条，则估计该河流中有野生鱼（）

A、8000条 B、4000条 C、2000条 D、1000条

查看试题解析
10. 以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（）

A、 $\frac{\sqrt{3}}{8}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{\sqrt{2}}{8}$

查看试题解析
11. 如图，在矩形ABCD中，AB=4，AD=5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线BC于点M，切点为N，则DM的长为（）

A、 $\frac{13}{3}$ B、 $\frac{9}{2}$ C、 $\frac{4}{3}$ $\sqrt{13}$ D、2 $\sqrt{5}$

查看试题解析
12. 如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= $\frac{6}{x}$ 在第一象限的图象经过点B，则△OAC与△BAD的面积之差S_△_OAC﹣S_△_BAD为（）

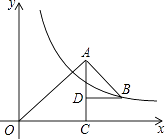A、36 B、12 C、6 D、3

查看试题解析

二、填空题

13. 如图△ABC是正三角形，曲线CDEF叫做“正三角形的渐开线”，其中 $\hat{C D}$ 、 $\hat{D E}$ 、 $\hat{E F}$ 圆心依次按A、B、C…循环，它们依次相连接．若AB=1，则曲线CDEF长是（结果保留π）．

查看试题解析
14. 若三角形的某一边长等于其外接圆半径，则将此三角形称为等径三角形，该边所对的角称为等径角．已知△ABC是等径三角形，则等径角的度数为

查看试题解析
15.
如图，点A、B是双曲线y= $\frac{3}{x}$ 上的点，分别经过A、B两点向x轴、y轴作垂线段，若S_阴影=1，则S₁+S₂=

查看试题解析
16. 某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是 cm．

查看试题解析

三、解答题

17. 今年“中秋”节前，朵朵的妈妈去超市购买了大小、形状、重量等都相同的五仁和豆沙月饼若干，放入不透明的盒中，此时从盒中随机取出五仁月饼的概率为 $\frac{1}{3}$ ；爸爸从盒中取出五仁月饼3只、豆沙月饼7只送给爷爷和奶奶后，这时随机取出五仁月饼的概率为 $\frac{2}{5}$ ．

(1)、请你用所学知识计算：妈妈买的五仁月饼和豆沙月饼各有多少只？

(2)、若朵朵一次从盒内剩余月饼中任取2只，问恰有五仁月饼、豆沙月饼各1只的概率是多少？（用列表法或树状图计算）

查看试题解析
18. 如图，在⊙O中，弦AB所对的劣弧是圆周长的 $\frac{1}{3}$ ，其中圆的半径为4cm，求：

(1)、求AB的长．

(2)、求阴影部分的面积．

查看试题解析
19. 某闭合电路中，其两端电压恒定，电流I（A）与电阻R（Ω）图象如图所示，回答问题：

(1)、写出电流I与电阻R之间的函数解析式．

(2)、如果一个用电器的电阻为5Ω，其允许通过的最大电流是1A，那么这个用电器接在这个闭合电路中，会不会烧毁？说明理由．

(3)、若允许的电流不超过4A时，那么电阻R的取值应该控制在什么范围？

查看试题解析
20. 如图，在△ABF中，以AB为直径的圆分别交边AF、BF于C、E两点，CD⊥AF．AC是∠DAB的平分线，

(1)、求证：直线CD是⊙O的切线．

(2)、求证：△FEC是等腰三角形．

查看试题解析
21. 阅读资料：我们把顶点在圆上，并且一边和圆相交、另一边和圆相切的角叫做弦切角，如图1∠ABC所示．同学们研究发现：P为圆上任意一点，当弦AC经过圆心O时，且AB切⊙O于点A，此时弦切角∠CAB=∠P（图2）
证明：∵AB切⊙O于点A，∴∠CAB=90°，又∵AC是直径，∴∠P=90°∴∠CAB=∠P

问题拓展：若AC不经过圆心O（如图3），该结论：弦切角∠CAB=∠P还成立吗？请说明理由．

知识运用：如图4，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F．求证：EF∥BC．

查看试题解析
22.
如图1，反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过点A（2 $\sqrt{3}$ ，1），射线AB与反比例函数图象交与另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．

(1)、求k和a的值；

(2)、直线AC的解析式；

(3)、
如图3，M是线段AC上方反比例函数图象上一动点，过M作直线l⊥x轴，与AC相交于N，连接CM，求△CMN面积的最大值．

查看试题解析