2016-2017学年山东省滨州市九年级上学期期中数学试卷
试卷更新日期：2017-01-20 类型：期中考试
一、选择题
-
1. 下列方程，是一元二次方程的是（ ）
①3x2+x=20，②2x2﹣3xy+4=0，③x2 =4，④x2=0，⑤x2﹣3x﹣4=0．
A、①② B、①②④⑤ C、①③④ D、①④⑤2. 如图，不是中心对称图形的是（ ）A、
B、
C、
D、
3. 若m是方程x2+x﹣1=0的根，则2m2+2m+2016的值为（ ）A、2016 B、2017 C、2018 D、20194. 一元二次方程2x2﹣3x+1=0根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 我省2014年的快递业务量为1.4亿件，受益于电子商务发展和法治环境改善等多重因素，快递业务迅猛发展，2016年的快递业务量达到4.5亿件．设2015年与2016年这两年的平均增长率为x，则下列方程正确的是（ ）A、1.4（1+x）=4.5 B、1.4（1+2x）=4.5 C、1.4（1+x）2=4.5 D、1.4（1+x）+1.4（1+x）2=4.56. 如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，∠A′B′C′可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为（ ）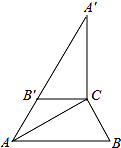
A、4 B、6 C、3 D、37. 如图，⊙O是△ABC的外接圆，已知∠ABO=40°，则∠ACB的大小为（ ）
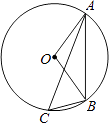A、40° B、30° C、45° D、50°8. 如图，AB是⊙O的弦，AC是⊙O切线，A为切点，BC经过圆心．若∠B=20°，则∠C的大小等于（ ）
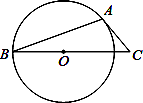A、20° B、25° C、40° D、50°9. 二次函数y=x2﹣2x+4化为y=a（x﹣h）2+k的形式，下列正确的是（ ）A、y=（x﹣1）2+2 B、y=（x﹣1）2+3 C、y=（x﹣2）2+2 D、y=（x﹣2）2+410. 点P1（﹣1，y1），P2（3，y2），P3（5，y3）均在二次函数y=﹣x2+2x+c的图象上，则y1 ， y2 ， y3的大小关系是（ ）A、y3＞y2＞y1 B、y3＞y1=y2 C、y1＞y2＞y3 D、y1=y2＞y311. 如图，⊙O的直径BD=6，∠A=60°，则BC的长度为（ ）
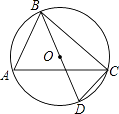A、 B、3 C、3 D、412. 如图是二次函数y=ax2+bx+c的图象的一部分，对称轴是直线x=1．①b2＞4ac；
②4a﹣2b+c＜0；
③不等式ax2+bx+c＞0的解集是x≥3.5；
④若（﹣2，y1），（5，y2）是抛物线上的两点，则y1＜y2 ．
上述4个判断中，正确的是（ ）
A、①② B、①④ C、①③④ D、②③④二、填空题
-
13. 抛物线y=（x+1）2﹣2的顶点坐标是 ．14. 将抛物线y=﹣x2先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为 ．15. 若关于x的一元二次方程x2﹣2x﹣k=0没有实数根，则k的取值范围是16.
如图是一个中心对称图形，A为对称中心，若∠C=90°，∠B=30°，BC=2 ，求BB′的长为
17. 如图，两同心圆的大圆半径长为5cm，小圆半径长为3cm，大圆的弦AB与小圆相切，切点为C，则弦AB的长是
18. 若规定两数a、b通过运算※得4ab，即a※b=4ab．如2※6=4×2×6=48．若x※x+2※x﹣2※4=0，则x的值为三、解答题
-
19. 综合题(1)、用公式法解方程x2﹣3x﹣7=0．(2)、解方程：4x（2x﹣1）=3（2x﹣1）20. 如图，已知△ABC的顶点A，B，C的坐标分别是A（﹣1，﹣1），B（﹣4，﹣3），C（﹣4，﹣1）．
（1）作出△ABC关于原点O中心对称的图形；
（2）将△ABC绕原点O按顺时针方向旋转90°后得到△A1B1C1 ， 画出△A1B1C1 ， 并写出点A1的坐标．21. 如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C．若AB是⊙O的直径，D是BC的中点．
(1)、试判断AB、AC之间的大小关系，并给出证明；(2)、在上述题设条件下，当△ABC为正三角形时，点E是否AC的中点？为什么？22. 已知关于x的方程x2﹣（2m+1）x+m2+m=0．(1)、求证：方程恒有两个不相等的实数根；(2)、设方程两实数根分别为x1 ， x2 ， 且满足x12+x22=3，求实数m的值．23. 如图所示，AB是⊙O的直径，点C是 的中点，∠COB=60°，过点C作CE⊥AD，交AD的延长线于点E
(1)、求证：CE为⊙O的切线；(2)、判断四边形AOCD是否为菱形？并说明理由．24. 如图，二次函数y=（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．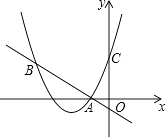
(1)、求二次函数与一次函数的解析式；(2)、根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．25. 2016年3月国际风筝节期间，王大伯决定销售一批风筝，经市场调研：蝙蝠型风筝进价每个为10元，当售价每个为12元时，销售量为180个，若售价每提高1元，销售量就会减少10个，请回答以下问题：(1)、用表达式表示蝙蝠型风筝销售量y（个）与售价x（元）之间的函数关系（12≤x≤30）；(2)、王大伯为了让利给顾客，并同时获得840元利润，售价应定为多少？(3)、当售价定为多少时，王大伯获得利润W最大，最大利润是多少？