2016-2017学年内蒙古巴彦淖尔市乌拉特前旗四中九年级上学期期中数学试卷
试卷更新日期：2017-01-20 类型：期中考试
一、选择题
-
1. 下列关于 x的方程：①ax2+bx+c=0；②x2+ =6；③x2=0；④x=3x2⑤（x+1）（x﹣1）=x2+4x中，一定是一元二次方程的个数是（ ）
A、1个 B、2个 C、3个 D、4个2. 下列标志既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 已知关于x的一元二次方程（a﹣1）x2﹣2x+1=0有两个不相等的实数根，则a的取值范围是（ ）A、a＞2 B、a＜2 C、a＜2且a≠l D、a＜﹣24. 若（2，5）、（4，5）是抛物线y=ax2+bx+c上的两个点，则它的对称轴是（ ）
A、x=﹣ B、x=1 C、x=2 D、x=35. 一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根，则该等腰三角形的周长是（ ）A、12 B、9 C、13 D、12或96.如图，某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分钟花草，要使每一块花草的面积都为78m2 ， 那么通道宽应设计成多少m？设通道宽为xm，则由题意列得方程为（ ）
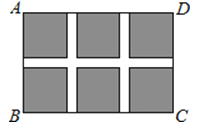A、（30﹣x）（20﹣x）=78 B、（30﹣2x）（20﹣2x）=78 C、（30﹣2x）（20﹣x）=6×78 D、（30﹣2x）（20﹣2x）=6×787.如图，△ABC为⊙O的内接三角形，∠AOB=100°，则∠ACB的度数为（ ）
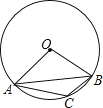A、100° B、130° C、150° D、160°8. 如图，在⊙O中，P是弦AB的中点，CD是过点P的直径，则下列结论中不正确的是（ ）
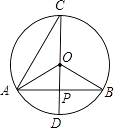A、AB⊥CD B、∠AOB=4∠ACD C、 = D、PO=PD9. 已知抛物线y=﹣x2+2x﹣3，下列判断正确的是（ ）A、开口方向向上，y有最小值是﹣2 B、抛物线与x轴有两个交点 C、顶点坐标是（﹣1，﹣2） D、当x＜1时，y随x增大而增大10. 有下列四个命题中，其中正确的有（ ）①圆的对称轴是直径；②等弦所对的弧相等；③圆心角相等所对的弦相等；④半径相等的两个半圆是等弧．
A、4个 B、3个 C、2个 D、1个11. 将抛物线y=3x2向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（ ）A、y=3（x+2）2+3 B、y=3（x﹣2）2+3 C、y=3（x+2）2﹣3 D、y=3（x﹣2）2﹣312. 下列说法正确的是（ ）A、弦是直径 B、平分弦的直径垂直弦 C、长度相等的两条弧是等弧 D、圆的对称轴有无数条，而对称中心只有一个13. 已知抛物线y=ax2+bx+c的开口向下，顶点坐标为（2，﹣3），那么该抛物线有（ ）A、最小值﹣3 B、最大值﹣3 C、最小值2 D、最大值2二、填空题
-
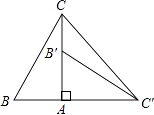
14. 钟表的时针匀速旋转一周需要12小时，经过2小时，时针旋转了度．15. 一元二次方程x2﹣4x+6=0实数根的情况是 ．16. 如图，在Rt△ABC中，∠BAC=90°，∠B=60°，△AB′C′可以由△ABC绕点A顺时针旋转90°得到（点B′与点B是对应点，点C′与点C是对应点），连接CC′，则∠CC′B′的度数是 ．
17. 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB的大小为
18. 已知二次函数y=ax2+bx+c的图象如图所示，有下列5个结论，①abc＜0； ②2a+b=0；③b2﹣4ac＜0；④a+b+c＞0；⑤a﹣b+c＜0．其中正确的结论有（填序号）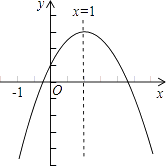
19. 分式 值为0，则x=20. 某商店四月份的利润为6.3万元，此后两个月进入淡季，利润均以相同的百分比下降，至六月份利润为5.4万元．设下降的百分比为x，由题意列出方程 ．21. 已知m是关于x的方程x2﹣2x﹣3=0的一个根，则2m2﹣4m= ．22. 下列图形中，①等腰三角形；②平行四边形；③等腰梯形；④圆；⑤正六边形；⑥菱形；⑦正五边形，是中心对称图形的有（填序号）23. 如图所示：点M、G、D在半圆O上，四边形OEDF、HMNO均为矩形，EF=b，NH=c，则b与c之间的大小关系是bc（填＜、=、＞）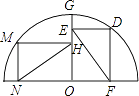
三、解下列方程
-
24. 解下列方程(1)、x2+6x﹣1=0(2)、（2x+3）2﹣25=0．
四、解答题
-
25. 在方格纸上建立如图所示的平面直角坐标系，将△ABO绕点O按顺时针方向旋转90°，得△A′B′O．
(1)、画出旋转后的图形；(2)、写出点A′，B′的坐标．26. 如图，是一圆柱形输水管的横截面，阴影部分为有水部分，如果水面宽8cm，水的最大深度为2cm，求该输水管的半径是多少？
27. 如图，在Rt△ABC中，∠ACB=90，AD平分∠BAC，过A，C，D三点的圆与斜边AB交于点E，连接DE．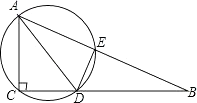
(1)、求证：AC=AE；(2)、若AC=6，CB=8，求△ACD的外接圆的直径．28.如图，已知抛物线与x交于A（﹣1，0）、E（3，0）两点，与y轴交于点B（0，3）．
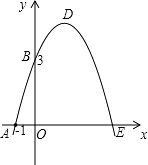(1)、求抛物线的解析式；(2)、设抛物线顶点为D，求四边形AEDB的面积．29. 某体育用品店购进一批单件为40元的球服，如果按单价60元销售样，那么一个月内可售出240套，根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高5元，销售量相应减少20套．设销售单价为x（x≥60）元，销售量为y套．(1)、求出y与x的函数关系式；(2)、当销售单件为多少元时，月销售额为14000元？(3)、当销售单价为多少元时，才能在一个月内获得最大利润？最大利润是多少？
-