2016-2017学年江苏省泰州市兴化市九年级上学期期中数学试卷
试卷更新日期:2017-01-20 类型:期中考试
一、选择题
-
1. 在20人的青年歌手比赛中,规定前10 名晋级,某个选手想知道自己能否晋级,应该选取( )A、平均数 B、众数 C、中位数 D、方差2. 某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为 甲=82分, 乙=82分,S甲2=245,S乙2=190,那么成绩较为整齐的是( )A、甲班 B、乙班 C、两班一样整齐 D、无法确定3. 用扇形统计图反应地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是108°,当宇宙中一块陨石落在地球上,则落在陆地上的概率是( )
 A、0.2 B、0.3 C、0.4 D、0.54. 已知二次函数y=(x﹣2)2+3,当自变量x分别取3、5、7时,y对应的值分别为y1、y2、y3 , 则y1、y2、y3的大小关系正确的是( )A、y3<y1<y2 B、y3<y2<y1 C、y2<y1<y3 D、y1<y2<y35. 根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )
A、0.2 B、0.3 C、0.4 D、0.54. 已知二次函数y=(x﹣2)2+3,当自变量x分别取3、5、7时,y对应的值分别为y1、y2、y3 , 则y1、y2、y3的大小关系正确的是( )A、y3<y1<y2 B、y3<y2<y1 C、y2<y1<y3 D、y1<y2<y35. 根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )x
3.23
3.24
3.25
3.26
ax2+bx+c
﹣0.06
﹣0.02
0.03
0.09
A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.266. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、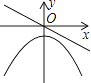 B、
B、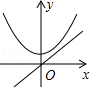 C、
C、 D、
D、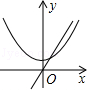
二、填空题
-
7. 五个数1,2,4,5,﹣2的极差是8. 抛掷一枚均匀的硬币2次,2次抛掷的结果都是正面朝上的概率为9. 数据3,2,1,5,﹣1,1的众数和中位数之和是10. 某工厂共有50名员工,他们的月工资方差s2=20,现在给每个员工的月工资增加300元,那么他们新工资的方差是 .11. 函数y=(m+2) +2x﹣1是二次函数,则m= .12. 某厂今年一月份新产品的研发资金为1000元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=13. 已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣ t2+20t+1.若此礼炮在升空到最高处时引爆,则引爆需要的时间为 .14. 把抛物线y=x2﹣2x向下平移2个单位长度,再向右平移1个单位长度,则平移后的抛物线相应的函数表达式为 .15. 某学校九(1)班40名同学的期中测试成绩分别为a1 , a2 , a3 , …,a40 . 已知a1+a2+a3+…+a40=4800,y=(a﹣a1)2+(a﹣a2)2+(a﹣a3)2+…+(a﹣a40)2 , 当y取最小值时,a的值为16. 若抛物线y=x2﹣4x+t(t为实数)在0≤x≤3的范围内与x轴有公共点,则t的取值范围为 .
三、解答题
-
17. 综合题(1)、已知二次函数y=ax2+bx+1的图象经过点(1,3)和(3,﹣5),求a、b的值;(2)、已知二次函数y=﹣x2+bx+c的图象与x轴的两个交点的横坐标分别为1和2.求这个二次函数的表达式.18. 甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
93
89
90
学生乙
94
92
94
86
(1)、分别计算甲、乙成绩的中位数;(2)、如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?19. 某市今年中考理、化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.(1)、用“列表法”或“树状图法”表示所有可能出现的结果;(2)、小刚抽到物理实验B和化学实验F(记作事件M)的概率是多少?20. 市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表(单位:环):第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)、根据表格中的数据,分别计算甲、乙的平均成绩;(2)、已知甲六次成绩的方差S甲2= ,试计算乙六次测试成绩的方差;根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
21. 在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是 .(1)、求暗箱中红球的个数.(2)、先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).22. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?23. 国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题: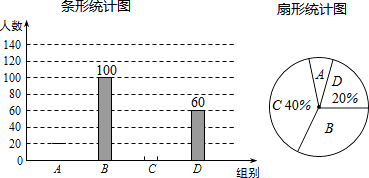 (1)、此次抽查的学生数为人,并补全条形统计图;(2)、从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是;(3)、若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人.24. 小明跳起投篮,球出手时离地面 m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.
(1)、此次抽查的学生数为人,并补全条形统计图;(2)、从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是;(3)、若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人.24. 小明跳起投篮,球出手时离地面 m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.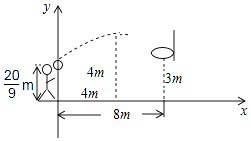 (1)、求此抛物线对应的函数关系式;(2)、此次投篮,球能否直接命中篮筐中心?若能,请说明理由;若不能,在出手的角度和力度都不变的情况下,球出手时距离地面多少米可使球直接命中篮筐中心?25. 已知二次函数y1=x2﹣6x+9﹣t2和一次函数y2=﹣2x﹣2t+6.(1)、当t=0时,试判断二次函数y1的图象与x轴是否有公共点,如果有,请写出公共点的坐标;(2)、若二次函数y1的图象与x轴的两个不同公共点,且这两个公共点间的距离为8,求t的值;(3)、求证:不论实数t取何值,总存在实数x,使y1≥ty2 .26. 在平面直角坐标系中,抛物线y=x2﹣6mx+5与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).(1)、当b=1时,求抛物线相应的函数表达式;(2)、当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(1)、求此抛物线对应的函数关系式;(2)、此次投篮,球能否直接命中篮筐中心?若能,请说明理由;若不能,在出手的角度和力度都不变的情况下,球出手时距离地面多少米可使球直接命中篮筐中心?25. 已知二次函数y1=x2﹣6x+9﹣t2和一次函数y2=﹣2x﹣2t+6.(1)、当t=0时,试判断二次函数y1的图象与x轴是否有公共点,如果有,请写出公共点的坐标;(2)、若二次函数y1的图象与x轴的两个不同公共点,且这两个公共点间的距离为8,求t的值;(3)、求证:不论实数t取何值,总存在实数x,使y1≥ty2 .26. 在平面直角坐标系中,抛物线y=x2﹣6mx+5与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).(1)、当b=1时,求抛物线相应的函数表达式;(2)、当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值; (3)、当c=b+n时,且n为正整数,线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.
(3)、当c=b+n时,且n为正整数,线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.