2016-2017学年湖北省武汉市江夏区九年级上学期期中数学试卷
试卷更新日期:2017-01-20 类型:期中考试
一、选择题
-
1. 随着我国经济快速发展,轿车进入百姓家庭,小明同学在街头观察出下列四种汽车标志,其中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程x2﹣3x﹣8=0的两根分别为x1、x2 , 则x1x2=( )A、2 B、﹣2 C、8 D、﹣83. 抛物线y=x2﹣2x+1与坐标轴交点个数为( )A、无交点 B、1个 C、2个 D、3个4. 如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
2. 一元二次方程x2﹣3x﹣8=0的两根分别为x1、x2 , 则x1x2=( )A、2 B、﹣2 C、8 D、﹣83. 抛物线y=x2﹣2x+1与坐标轴交点个数为( )A、无交点 B、1个 C、2个 D、3个4. 如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( ) A、5 B、7 C、9 D、115. 若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )A、k<5 B、k<5,且k≠1 C、k≤5,且k≠1 D、k>56. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
A、5 B、7 C、9 D、115. 若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )A、k<5 B、k<5,且k≠1 C、k≤5,且k≠1 D、k>56. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )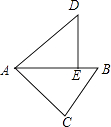 A、 B、2 C、3 D、27. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式CH4 , 乙烷的化学式是C2H6 , 丙烷的化学式是C3H8 , …,设碳原子的数目为n(n为正整数),则它们的化学式都可以用下列哪个式子来表示( )A、CnH2n+2 B、CnH2n C、CnH2n﹣2 D、CnHn+38. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )A、
A、 B、2 C、3 D、27. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式CH4 , 乙烷的化学式是C2H6 , 丙烷的化学式是C3H8 , …,设碳原子的数目为n(n为正整数),则它们的化学式都可以用下列哪个式子来表示( )A、CnH2n+2 B、CnH2n C、CnH2n﹣2 D、CnHn+38. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )A、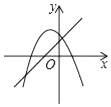 B、
B、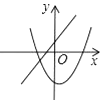 C、
C、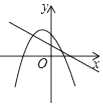 D、
D、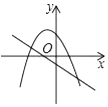 9. O是等边△ABC内的一点,OB=1,OA=2,∠AOB=150°,则OC的长为( )
9. O是等边△ABC内的一点,OB=1,OA=2,∠AOB=150°,则OC的长为( )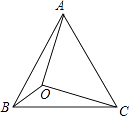 A、 B、 C、 D、3
A、 B、 C、 D、3二、填空题
-
10. 构造一个根为2和3的一元二次方程(写一个即可,不限形式)11. 某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,若干小分支、支干和主干的总数是73,则每个支干长出个小分支.12. 已知A(0,3)、B(2,3)是抛物线y=﹣x2+bx+c上两点,该抛物线的对称轴是 .13. 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE= .
 14. 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是
14. 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是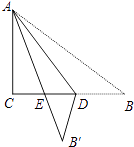 15. 函数y= 的图象与直线y=﹣x+n只有两个不同的公共点,则n的取值为 .
15. 函数y= 的图象与直线y=﹣x+n只有两个不同的公共点,则n的取值为 .三、解答题
-
16. 解方程:x2+4x﹣5=0.17. 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
 18. 江夏某村种植的水稻2010年平均亩产500kg,2012年平均亩产605kg,求该村亩产量的年平均增长率.19. 如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4)
18. 江夏某村种植的水稻2010年平均亩产500kg,2012年平均亩产605kg,求该村亩产量的年平均增长率.19. 如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4) (1)、请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1 , 直接写出点A1的坐标;(2)、请画出△ABC绕原点O顺时针旋转90°的图形△A2B2C2 , 直接写出点A2的坐标;(3)、在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.20. 已知:关于x的方程x2+(8﹣4m)x+4m2=0(1)、若方程有两个相等的实数根,求m的值,并求出此时方程的根;(2)、是否存在实数m,使方程的两个实数根的平方和等于136?若存在,请求出满足条件的m值;若不存在,请说明理由.21. 某商场销售的某种商品每件的标价是80元,若按标价的八折销售,仍可盈利60%,此时该种商品每星期可卖出220件,市场调查发现:在八折销售的基础上,该种商品每降价1元,每星期可多卖20件.设每件商品降价x元(x为整数),每星期的利润为y元(1)、求该种商品每件的进价为多少元?(2)、当售价为多少时,每星期的利润最大?最大利润是多少?(3)、2015年2月该种商品每星期的售价均为每件m元,若2015年2月的利润不低于24000元,请直接写出m的取值范围.22.
(1)、请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1 , 直接写出点A1的坐标;(2)、请画出△ABC绕原点O顺时针旋转90°的图形△A2B2C2 , 直接写出点A2的坐标;(3)、在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.20. 已知:关于x的方程x2+(8﹣4m)x+4m2=0(1)、若方程有两个相等的实数根,求m的值,并求出此时方程的根;(2)、是否存在实数m,使方程的两个实数根的平方和等于136?若存在,请求出满足条件的m值;若不存在,请说明理由.21. 某商场销售的某种商品每件的标价是80元,若按标价的八折销售,仍可盈利60%,此时该种商品每星期可卖出220件,市场调查发现:在八折销售的基础上,该种商品每降价1元,每星期可多卖20件.设每件商品降价x元(x为整数),每星期的利润为y元(1)、求该种商品每件的进价为多少元?(2)、当售价为多少时,每星期的利润最大?最大利润是多少?(3)、2015年2月该种商品每星期的售价均为每件m元,若2015年2月的利润不低于24000元,请直接写出m的取值范围.22.如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
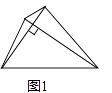 (1)、
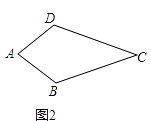
(1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
 (2)、性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
(2)、性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)、问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
 23.
23.如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C
 (1)、求A、B、C的坐标;(2)、过抛物线上一点F作y轴的平行线,与直线AC交于点G.若FG= AC,求点F的坐标;(3)、E(0,﹣2),连接BE.将△OBE绕平面内的某点逆时针旋转90°得到△O′B′E′,O、B、E的对应点分别为O′、B′、E′.若点B′、E′两点恰好落在抛物线上,求点B′的坐标.
(1)、求A、B、C的坐标;(2)、过抛物线上一点F作y轴的平行线,与直线AC交于点G.若FG= AC,求点F的坐标;(3)、E(0,﹣2),连接BE.将△OBE绕平面内的某点逆时针旋转90°得到△O′B′E′,O、B、E的对应点分别为O′、B′、E′.若点B′、E′两点恰好落在抛物线上,求点B′的坐标.