2016-2017学年湖北省黄冈市蕲春县九年级上学期期中数学试卷

试卷更新日期：2017-01-20 类型：期中考试

进入出卷网下载

一、填空题

1. 已知1是关于x的一元二次方程x²+mx+n=0的一个根，那么m+n=

查看试题解析
2. 平面直角坐标系中，一点P（﹣2，3）关于原点的对称点P′的坐标是

查看试题解析
3. 抛物线y=2x²﹣3x+4与y轴的交点坐标是．

查看试题解析
4. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x= ．

查看试题解析
5. 已知抛物线y=ax²+bx+c（a≠0）与x轴交于A，B两点，若点A的坐标为（﹣2，0），抛物线的对称轴为直线x=2，则线段AB的长为

查看试题解析
6. 如图，有正方形ABCD，把△ADE顺时针旋转到△ABF的位置．其中AD=4，AE=5，则BF=

查看试题解析
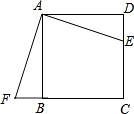7. 如图，AB是⊙O的弦，OC⊥AB于点C，若AB=4cm，OC=2cm，则⊙O的半径长是．

查看试题解析
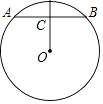8. 刘谦的魔术表演风靡全国，小明也学起了刘谦发明了一个魔术盒，当任意实数对（a，b）进入其中时，会得到一个新的实数：a²+b﹣1，例如把（3，﹣2）放入其中，就会得到3²+（﹣2）﹣1=6．现将实数对（m，﹣2m）放入其中，得到实数2，则m= ．

查看试题解析
9. 已知二次函数y₁=ax²+bx+c与一次函数y₂=kx+m（k≠0）的图象相交于点A（﹣2，4），B（8，2）．如图所示，则能使y₁＞y₂成立的x的取值范围是

查看试题解析
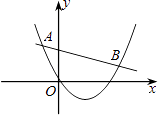10. 在如图所示的平面直角坐标系中，△OA₁B₁是边长为2的等边三角形，作△B₂A₂B₁与△OA₁B₁关于点B₁成中心对称，再作△B₂A₃B₃与△B₂A₂B₁关于点B₂成中心对称，…，如此作下去，则△B₂₀₁₅A₂₀₁₆B₂₀₁₆的顶点A₂₀₁₆的坐标是．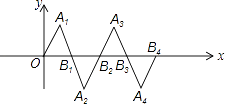

查看试题解析

二、选择题

11. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
12. 关于x的一元二次方程x²﹣6x+2k=0有两个不相等的实数根，则实数k的取值范围是（）

A、 $k \leq \frac{9}{2}$ B、 $k < \frac{9}{2}$ C、 $k \geq \frac{9}{2}$ D、 $k > \frac{9}{2}$

查看试题解析
13. 已知函数 y=（m+2） $x^{m^{2} - 2}$ 是二次函数，则m等于（）

A、±2 B、2 C、﹣2 D、±1

查看试题解析
14. 如图，将△ABC绕点P顺时针旋转90^o得到△A'B'C'，则点P的坐标是（）

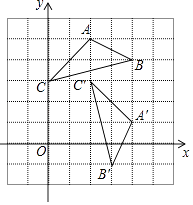A、（1，1） B、（1，2） C、（1，3） D、（1，4）

查看试题解析
15. 抛物线y=3x²先向上平移2个单位，再向右平移3个单位，所得的抛物线为（）

A、y=3（x+3）²﹣2 B、y=3（x+3）²+2 C、y=3（x﹣3）²﹣2 D、y=3（x﹣3）²+2

查看试题解析
16. 如图，A、B、C是⊙O上的三点，已知∠O=60°，则∠C=（）

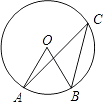A、20° B、25° C、30° D、45°

查看试题解析
17. 如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=8，则OP的长为（）

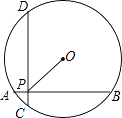A、3 B、4 C、3 $\sqrt{2}$ D、4 $\sqrt{2}$

查看试题解析
18. 已知关于x的方程x²+bx+a=0的一个根是﹣a（a≠0），则a﹣b值为（）

A、﹣1 B、0 C、1 D、2

查看试题解析
19. 给出下列四个函数：①y=﹣x；②y=x；③y=﹣x²；④y=x² ．当x＜0时，y随x的增大而减小的函数有（）

A、①③ B、①④ C、②③ D、②④

查看试题解析
20. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，对称轴是直线x=﹣1，下列结论：
①abc＜0；②2a+b=0；③a﹣b+c＞0；④4a﹣2b+c＜0
其中正确的是（）

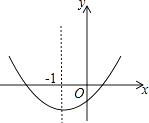A、①② B、只有① C、③④ D、①④

查看试题解析

三、解答题．

21. 解下列方程：

(1)、x（x﹣3）+x﹣3=0

(2)、x²﹣4x+1=0．

查看试题解析
22. 如图，在平面直角坐标系中，A（0，1），B（﹣3，5），C（﹣3，1）．

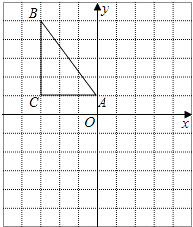(1)、在图中画出△ABC以A为旋转中心，沿顺时针方向旋转90^o后的图形△AB₁C₁ ，并写出B₁、C₁两点的坐标；

(2)、在图中画出与△ABC关于原点对称的图形△A₂B₂C₂ ，并写出B₂、C₂两点的坐标．

查看试题解析
23. 已知二次函数的顶点坐标为（1，4），且其图象经过点（﹣2，﹣5），求此二次函数的解析式．

查看试题解析
24. 已知关于x的一元二次方程（a+c）x²+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．

(1)、如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；

(2)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

(3)、如果△ABC是等边三角形，试求这个一元二次方程的根．

查看试题解析
25. 如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．

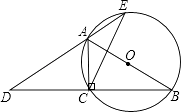(1)、求证：∠B=∠D；

(2)、若AB=4，BC﹣AC=2，求CE的长．

查看试题解析
26. 某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价一元，日销售量将减少20千克．

(1)、现要保证每天盈利6000元，同时又要让顾客得到实惠，那么每千克应涨价多少元？

(2)、若该商场单纯从经济角度看，那么每千克应涨价多少元，能使商场获利最多．

查看试题解析
27.
如图，抛物线y=﹣x²+bx+c交x轴于点A（﹣3，0）和点B，交y轴于点C（0，3）．

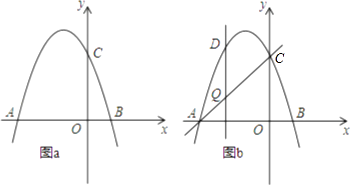(1)、求抛物线的函数表达式；

(2)、若点P在抛物线上，且S_△_AOP=4S_BOC ，求点P的坐标；

(3)、如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值

查看试题解析