浙江省温州市乐清市2017-2018学年八年级下学期期末考试试卷
试卷更新日期:2018-07-05 类型:期末考试
一、选择题
-
1. 若二次根式 有意义,则x的取值范围是( )
A、x≥-5 B、x>-5 C、x≥5 D、x>52. 方程x(x-6)=0的根是( )
A、x1=0,x2=-6 B、x1=0,x2=6 C、x=6 D、x=03. 某校5个小组参加植树活动,平均每组植树10株.已知第一,二,三,五组分别植树9株、12株、9株、8株,那么第四小组植树( )A、12株 B、11株 C、10株 D、9株4. 在四边形ABCD中,∠A,∠B,∠C,∠D度数之比为1:2:3:3,则∠B的度数为( )
A、30° B、40° C、80° D、120°5. 对于命题“已知:a∥b,b∥c,求证:a∥c”.如果用反证法,应先假设( )
A、a不平行b B、b不平行c C、a⊥c D、a不平行c6. 已知点P(1,-3)在反比例函数 (k≠0)的图象上,则k的值是( )
A、3 B、 C、-3 D、7. 如图,在▱ABCD中,对角线AC与BD交于点D,若增加一个条件,使▱ABCD成为菱形,下列给出的条件正确的是( )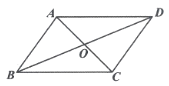 A、AB=AD B、AC=BD C、∠ABC=90° D、∠ABC=∠ADC8. 在▱ABCD中,对角线AC,BD相交于点O,AC=8,BD=10,那么BC的取值范围是( )A、8<BC<10 B、2<BC<18 C、1<BC<8 D、1<BC<99. 如图,在正方形ABCD外侧,作等边△ADE,AC,BE相交于点F,则∠BFC为( )
A、AB=AD B、AC=BD C、∠ABC=90° D、∠ABC=∠ADC8. 在▱ABCD中,对角线AC,BD相交于点O,AC=8,BD=10,那么BC的取值范围是( )A、8<BC<10 B、2<BC<18 C、1<BC<8 D、1<BC<99. 如图,在正方形ABCD外侧,作等边△ADE,AC,BE相交于点F,则∠BFC为( ) A、75° B、60° C、55° D、45°10. 已知图2是由图1七巧板拼成的数字“0”,已知正方形ABCD的边长为4,则六边形EFGHMN的周长为( )
A、75° B、60° C、55° D、45°10. 已知图2是由图1七巧板拼成的数字“0”,已知正方形ABCD的边长为4,则六边形EFGHMN的周长为( )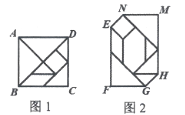 A、 B、 C、 D、12
A、 B、 C、 D、12二、填空题
-
11. 当x=2时,二次根式 的值为 .
12. 四边形的外角和是度.13. 如图,在△ABC中,点D,E分别是BC,AC的中点,AB=8,则DE的长为。 14. 若一元二次方程x2-2x+a=0有两个相等的实数根,则a的值是 .
14. 若一元二次方程x2-2x+a=0有两个相等的实数根,则a的值是 .
15. 如图,在▱ABCD中,AB=2,BC=3,∠BAD=120°,AE平分∠BAD,交BC于点E,过点C作CF∥AE,交AD于点F,则四边形AECF的面积为 .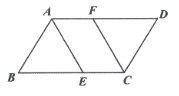 16. 如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴上,且点A坐标为(0,4),BC在x轴正半轴上,点C在B点右侧,反比例函数 (x>0)的图象分别交边AD,CD于E,F,连结BF,已知,BC=k,AE= CF,且S四边形ABFD=20,则k= .
16. 如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴上,且点A坐标为(0,4),BC在x轴正半轴上,点C在B点右侧,反比例函数 (x>0)的图象分别交边AD,CD于E,F,连结BF,已知,BC=k,AE= CF,且S四边形ABFD=20,则k= .
三、解答题
-
17.(1)、计算:(2)、解方程:x2+2x-3=018. 在学校组织的知识竞赛中,八(1)班比赛成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩整理并绘制成如下的统计图.

请你根据以上提供的信息解答下列问题:
(1)、请根据统计图的信息求出成绩为C等级的人数。(2)、将表格补充完整.班级
平均分(分)
中位数(分)
众数(分)
八(1)
87.6
19. 已知:如图,▱ABCD的对角线AC,BD相交于0,点E,F分别在AO,CO上,且AE=CF,求证:四边形BEDF是平行四边形. 20. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,6),请在所给网格区域(含边界)上按要求画整点四边形.
20. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,6),请在所给网格区域(含边界)上按要求画整点四边形. (1)、在图1中画一个整点四边形ABCD,四边形是轴对称图形,且面积为10;
(1)、在图1中画一个整点四边形ABCD,四边形是轴对称图形,且面积为10;
(2)、在图2中画一个整点四边形ABCD,四边形是中心对称图形,且有两个顶点各自的横坐标比纵坐标小1.
21. 如图,在平面直角坐标系中,直线EF交x,y轴子点F,E,交反比例函数 (x>0)图象于点C,D,OE=OF= ,以CD为边作矩形ABCD,顶点A与B恰好落在y轴与x轴上. (1)、若矩形ABCD是正方形,求CD的长。(2)、若AD:DC=2:1,求k的值.22. 小明家准备给边长为6m的正方形客厅用黑色和白色两种瓷砖铺设,如图所示:①黑色瓷砖区域Ⅰ:位于四个角的边长相同的小正方形及宽度相等的回字型边框(阴影部分),②白色瓷砖区域Ⅱ:四个全等的长方形及客厅中心的正方形(空白部分).设四个角上的小正方形的边长为x(m).
(1)、若矩形ABCD是正方形,求CD的长。(2)、若AD:DC=2:1,求k的值.22. 小明家准备给边长为6m的正方形客厅用黑色和白色两种瓷砖铺设,如图所示:①黑色瓷砖区域Ⅰ:位于四个角的边长相同的小正方形及宽度相等的回字型边框(阴影部分),②白色瓷砖区域Ⅱ:四个全等的长方形及客厅中心的正方形(空白部分).设四个角上的小正方形的边长为x(m). (1)、当x=0.8时,若客厅中心的正方形瓷砖铺设的面积为16m2 , 求回字型黑色边框的宽度;
(1)、当x=0.8时,若客厅中心的正方形瓷砖铺设的面积为16m2 , 求回字型黑色边框的宽度;
(2)、若客厅中心的正方形边长为4m,白色瓷砖区域Ⅱ的总面积为26m2 , 求x的值.
23. 如图1,在矩形ABCD中,AB=4,AD=5,E为射线BC上一点,DF⊥AE于F,连结DE. (1)、当E在线段BC上时
(1)、当E在线段BC上时①若DE=5,求BE的长;
②若CE=EF,求证:AD=AE;
(2)、连结BF,在点E的运动过程中:①当△ABF是以AB为底的等腰三角形时,求BE的长;
②记△ADF的面积为S1 , 记△DCE的面积为S2 , 当BF∥DE时,请直接写出S1:S2的值.