江苏省南通市2018年中考数学试卷
试卷更新日期:2018-07-05 类型:中考真卷
一、选择题
-
1. 的值是( )A、4 B、2 C、 D、2. 下列计算中,正确的是( )A、 B、 C、 D、3. 若 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、4. 函数 的图象与函数 的图象的交点在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列说法中,正确的是( )A、—个游戏中奖的概率是 ,则做10次这样的游戏一定会中奖 B、为了了解一批炮弹的杀伤半径,应采用全面调查的方式 C、一组数据8,8,7,10,6,8,9的众数是8 D、若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小6. 篮球比赛规定:胜一场得3分,负一场得1分.某篮球队共进行了 6场比赛,得了 12分,该队获胜的场数是( )
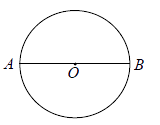
A、2 B、3 C、4 D、57. 如图, ,以点 为圆心,小于 长为半径作圆弧,分别交 于点 ,再分别以 为圆心,大于 的同样长为半径作圆弧,两弧交于点 ,作射线 ,交 于点 .若 ,则 的度数为( ) A、 B、 C、 D、8. —个空间几何体的主视图和左视图都是边长为 的正三角形,俯视图是一个圆,那么这个几何体的表面积是( )
A、 B、 C、 D、8. —个空间几何体的主视图和左视图都是边长为 的正三角形,俯视图是一个圆,那么这个几何体的表面积是( )
A、 B、 C、 D、9. 如图,等边 的边长为 ,动点 从点 出发,以每秒 的速度,沿 的方向运动,到达点 时停止,设运动时间为 , ,则 关于 的函数的图象大致为( )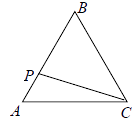 A、
A、 B、
B、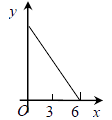 C、
C、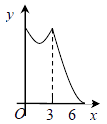 D、
D、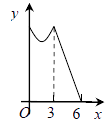 10. 正方形 的边长 , 为 的中点, 为 的中点, 分别与 相交于点 ,则 的长为( )
10. 正方形 的边长 , 为 的中点, 为 的中点, 分别与 相交于点 ,则 的长为( )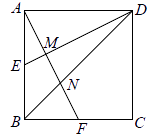 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. “辽宁舰”最大排水量为67500吨,将67500用科学记数法表示为 .12. 分解因式: .13. 正 边形的一个内角为135° ,则 .
14. 某厂一月份生产某机器100台,计划三月份生产160台.设二、三月份每月的平均增长率为 ,根据题意列出的方程是 .
15. 如图, 是 的直径,点 是 上的一点,若 , 于点 ,则 的长为 . 16. 下面是“作一个 角”的尺规作图过程.
16. 下面是“作一个 角”的尺规作图过程.已知:平面内一点 .
求作: ,使得 .
作法:如图,

①作射线 ;
②在射线 上取一点 ,以 为圆心, 为半径作圆,与射线 相交于点 ;
③以 为圆心, 为半径作孤,与 交于点 ,作射线 . 即为所求的角.
请回答:该尺规作图的依据是 .
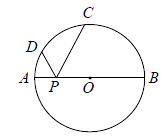
17. 如图,在 中,∠C=90°,AC=3,BC=4,点 是 中点,将 绕点 旋转得 ,则在旋转过程中点 两点间的最大距离是 . 18. 在平面直角坐标系 中,过点 作垂直于 轴的直线 ,直线 与双曲线 交于点 , 与直线 交于点 ,若 时,则 的取值范围是 .
18. 在平面直角坐标系 中,过点 作垂直于 轴的直线 ,直线 与双曲线 交于点 , 与直线 交于点 ,若 时,则 的取值范围是 .
三、解答题
-
19.
(1)、计算: ;
(2)、解方程: .20. 解不等式组 ,并写出 的所有整数解.21. “校园安全”受到全社会的广泛关注.某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请根据统计图中所提供的信息解答下列问题:

 (1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应扇形的圆心角为度;(2)、请补全条形统计图;(3)、若该中学共有学生1200人,估计该中学学生对校园安全知识达到“了解”和“基本了解” 程度的总人数.22. 四张扑克牌的点数分别是2, 3, 4, 8,除点数不同外,其余都相同,将它们洗匀后背面朝上放在桌上.(1)、从中随机抽取一张牌,求这张牌的点数是偶数的概率;(2)、随机抽取一张牌不放回,接着再抽取一张牌,求这两张牌的点数都是偶数的概率.23. 如图,小明一家自驾到古镇 游玩,到达 地后,导航显示车辆应沿北偏西 方向行驶12 千米至 地,再沿北偏东 方向行驶一段距离到达古镇 ,小明发现古镇 恰好在 地的正北方向,求 两地的距离.(结果保留根号)
(1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应扇形的圆心角为度;(2)、请补全条形统计图;(3)、若该中学共有学生1200人,估计该中学学生对校园安全知识达到“了解”和“基本了解” 程度的总人数.22. 四张扑克牌的点数分别是2, 3, 4, 8,除点数不同外,其余都相同,将它们洗匀后背面朝上放在桌上.(1)、从中随机抽取一张牌,求这张牌的点数是偶数的概率;(2)、随机抽取一张牌不放回,接着再抽取一张牌,求这两张牌的点数都是偶数的概率.23. 如图,小明一家自驾到古镇 游玩,到达 地后,导航显示车辆应沿北偏西 方向行驶12 千米至 地,再沿北偏东 方向行驶一段距离到达古镇 ,小明发现古镇 恰好在 地的正北方向,求 两地的距离.(结果保留根号) 24. 如图, 中,点 是 的中点,连接 并延长交 延长线于点 .
24. 如图, 中,点 是 的中点,连接 并延长交 延长线于点 .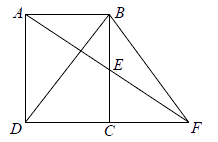 (1)、求证: ;(2)、连接 ,当 时,求证: .25. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为 ,两车之间的距离为 ,图中的折线表示 与 之间的函数关系.根据图象解决以下问题:
(1)、求证: ;(2)、连接 ,当 时,求证: .25. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为 ,两车之间的距离为 ,图中的折线表示 与 之间的函数关系.根据图象解决以下问题: (1)、慢车的速度为 ,快车的速度为 ;
(1)、慢车的速度为 ,快车的速度为 ;
(2)、解释图中点 的实际意义,并求出点 的坐标;
(3)、求当 为多少时,两车之间的距离为500 .
26. 如图, 中, ,点 以 的速度从点 出发沿边 运动到点 停止,运动时间为 ,点 是线段 的中点.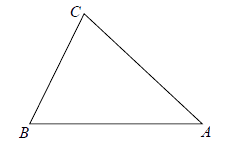 (1)、若 时,求 的值;(2)、若 是直角三角形时,求 的值;(3)、设 的面积为 ,求 与 的关系式,并写出 的取值范围.
(1)、若 时,求 的值;(2)、若 是直角三角形时,求 的值;(3)、设 的面积为 ,求 与 的关系式,并写出 的取值范围.