浙江省2018年小学数学毕业模拟考试模拟卷 10
试卷更新日期:2018-07-05 类型:小升初模拟
一、填空题
-
1. 1590949000读作 , 用“万”作单位省略后面的尾数是 , 用“亿”作单位保留一位小数约是。
2.
3. 在下面的括号中填上单位名称或数。12时12分=时
一瓶牛奶的容积约是220
1 公顷=平方米
数学书封面的面积大约是3
4. 把3千克白糖平均装在m只袋子里,每袋重千克,2袋占总重量的。(m>3)
5. 右图中B点在(4,2),那么A点在 , 以AB所在的直线为对称轴,C点的对称点C'的位置是。 6. 一个长方体的体积为175立方厘米,它的棱长都是质数,那么这个长方体的棱长总和是厘米。7. 一个小贩做月饼买卖,进价是2元5个,售价是3元4个,某天恰好赚700元,这大他一共卖出只月饼。8. 如图,把一个用草绳编织成的圆形垫片沿直径剪开,再把其中一个半圆沿半径r剪成相等的两份,拼成一个近似的长方形。长方形的长相当于 , 宽相当于。如果长方形的长是31.4厘米,那么这个圆的面积是平方厘米。
6. 一个长方体的体积为175立方厘米,它的棱长都是质数,那么这个长方体的棱长总和是厘米。7. 一个小贩做月饼买卖,进价是2元5个,售价是3元4个,某天恰好赚700元,这大他一共卖出只月饼。8. 如图,把一个用草绳编织成的圆形垫片沿直径剪开,再把其中一个半圆沿半径r剪成相等的两份,拼成一个近似的长方形。长方形的长相当于 , 宽相当于。如果长方形的长是31.4厘米,那么这个圆的面积是平方厘米。 9. 观察右图推算:一个小球的体积是立方厘米。
9. 观察右图推算:一个小球的体积是立方厘米。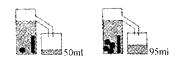 10. 观察下图分别有几个三角形,并用发现的规律填空:
10. 观察下图分别有几个三角形,并用发现的规律填空: (1)、第四个图形中三角形有个。(2)、第行个图形中三角形有个。
(1)、第四个图形中三角形有个。(2)、第行个图形中三角形有个。二、选择题
-
11. 下列百分率中,有可能超过100%的是( )。A、出油率 B、增长率 C、成活率 D、正确率12. 一堆煤,用去 后,还剩下 吨,这堆煤原有( )吨。A、 B、 C、1 D、213. 100张纸叠起来的高度约是1厘米,那么1亿张纸叠起来和( )的高度最接近。A、一个人 B、旗杆 C、100层摩天大楼 D、珠穆朗玛峰14. 下面各题中,( )成反比例关系。A、圆的周长和直径 B、圆的半径和面积 C、长方形的面积一定,它的长和宽 D、梯形的周长一定,它的上底和下底15. 肖勇和妹妹一起去上学,途中肖勇发现忘带作业本,于是他跑回家,拿好作业本,马上向学校飞奔而去,刚好在校门口追上了妹妹,下面哪幅图描述的是肖勇和妹妹上学路上的情景( )。
A、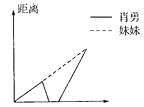 B、
B、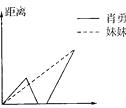 C、
C、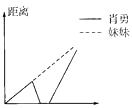 D、
D、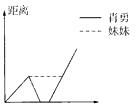 16. 读幼儿园的张浩发现家里有一张身份证,号码是:330224194812210035,这有可能是他( )的身份证。A、爸爸 B、妈妈 C、爷爷 D、奶奶17. 下图不能用“底面积×高”计算体积的是( )。A、
16. 读幼儿园的张浩发现家里有一张身份证,号码是:330224194812210035,这有可能是他( )的身份证。A、爸爸 B、妈妈 C、爷爷 D、奶奶17. 下图不能用“底面积×高”计算体积的是( )。A、 B、
B、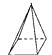 C、
C、 D、
D、 18. 关于三角形,下列说法错误的是( )。A、三角形不容易变形 B、任意一个三角形,内角和都是180。 C、三角形可以分为:锐角三角形,直角三焦形,钝角三角形 D、5厘米,5厘米,10厘米长的三根小棒,能围成一个等腰三角形19. 下列说法正确的有( )句。
18. 关于三角形,下列说法错误的是( )。A、三角形不容易变形 B、任意一个三角形,内角和都是180。 C、三角形可以分为:锐角三角形,直角三焦形,钝角三角形 D、5厘米,5厘米,10厘米长的三根小棒,能围成一个等腰三角形19. 下列说法正确的有( )句。①0.4与0.6之间的小数只有0.5。
②一个两位小数精确到十分位后约是10.0,这个小数最大是10.04。
③用三个1,两个0组成的最小三位小数是10.101。
④在3.08的小数点后面加上一个0,小数的大小不变。
A、1 B、2 C、3 D、420. 图中阴影部分的面积是3平方厘米.那么圆环的面积是( )平方厘米。 A、9.42 B、9 C、18.84 D、无法知道
A、9.42 B、9 C、18.84 D、无法知道三、计算题
-
21. 直接写出得数。
1127-998=
15 0.01= 4.2+8=
42 =
22. 递等式计算,能简便的要简便计算。
(1)、630+270÷18×15=
(2)、(3)、(4)、 =(5)、 =(6)、 =23. 求未知数x
(1)、2.4 5-2x=9(2)、x- x=(3)、0.4: =x:2024. 列式计算。
(1)、36的 加上14的40%和是多少?(2)、甲数是15,比乙数的30%多2.4,求乙数。25. 图形计算。
(1)、把右边的梯形沿虚线BE分成面积相等的两部分,求AE的长。(单位:米) (2)、将梯形绕直线a旋转一周,求所形成的立体图形的体积。
(2)、将梯形绕直线a旋转一周,求所形成的立体图形的体积。
四、解答题
-
26. 据浙江省水文局的记录,去年第一季度我省平均降水量为660毫米,今年同期比去年减少53%,第一季度我省平均降水量为多少毫米?27. 图书馆里童话书和连环画各有多少本?(用方程解)
 28. 一张圆桌的直径达到1.8米,按照每人占有位置70厘米计算(如图),这张圆桌大约可以坐几个人?
28. 一张圆桌的直径达到1.8米,按照每人占有位置70厘米计算(如图),这张圆桌大约可以坐几个人? 29. 一个直角三角形的周长是36厘米,三条边的长度之比是3:4:5。(1)、这个三角形三条边长分别是几厘米?(2)、这个直角三角形的面积是多少平方厘米?30. 某市女力开学新能源。造成了各种新能源发电厂,改变了过去完全依赖煤炭发电的现象:
29. 一个直角三角形的周长是36厘米,三条边的长度之比是3:4:5。(1)、这个三角形三条边长分别是几厘米?(2)、这个直角三角形的面积是多少平方厘米?30. 某市女力开学新能源。造成了各种新能源发电厂,改变了过去完全依赖煤炭发电的现象: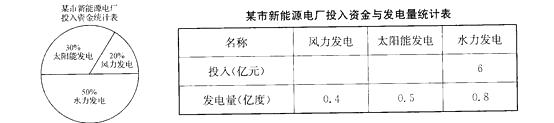 (1)、求出风力发电和太阳能发电的投入,并填到表中。(2)、已知这三类新能源发电量占该地区发电总量的17%,求该地区的发电总量。31. 有一只渔船在“救援中心”东偏北30。方向的180千米处触礁遇险,预计2小时后将沉没。救援中心有2条搜救船,时速均为80千米/小时。此时甲搜救船正在“救援中心”北偏东30。方向的120千米处巡逻;乙搜救船在“救援中心”待命……
(1)、求出风力发电和太阳能发电的投入,并填到表中。(2)、已知这三类新能源发电量占该地区发电总量的17%,求该地区的发电总量。31. 有一只渔船在“救援中心”东偏北30。方向的180千米处触礁遇险,预计2小时后将沉没。救援中心有2条搜救船,时速均为80千米/小时。此时甲搜救船正在“救援中心”北偏东30。方向的120千米处巡逻;乙搜救船在“救援中心”待命…… (1)、在右图中按比例画出遇险船和甲搜救船的具体位置。(2)、你认为该派哪艘船救援?它能否及时赶到遇险地点?(请你在必要的测量后,用计算来表明。)
(1)、在右图中按比例画出遇险船和甲搜救船的具体位置。(2)、你认为该派哪艘船救援?它能否及时赶到遇险地点?(请你在必要的测量后,用计算来表明。)