2016年浙江省宁波市鄞州区中考数学一模试卷

试卷更新日期：2017-01-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列四个实数中，最小的是（）

A、﹣3 B、﹣π C、﹣ $\sqrt{5}$ D、0

查看试题解析
2. 据统计2015年宁波市实现地区生产总值8011.5亿元，按可比价格计算，比上年增长了8%，把8011.5亿用科学记数法表示是（）

A、8011.5×10⁸ B、801.15×10⁹ C、8.0115×10¹⁰ D、8.0115×10¹¹

查看试题解析
3. 下列运算正确的是（）

A、a²×a³=a⁶ B、a²+a²=2a⁴ C、a⁸÷a⁴=a⁴ D、（a²）³=a⁵

查看试题解析
4. 如图中几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列图形中，轴对称图形有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 从长度分别为2，4，6，7的四条线段中随机取三条，能构成三角形的概率是（　　）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
7. 圆锥的截面是一个等边三角形，则它的侧面展开图圆心角度数是（）

A、60° B、90° C、120° D、180°

查看试题解析
8. 已知菱形的边长和一条对角线的长均为2cm，则菱形的面积为（）

A、3cm² B、4cm² C、 $\sqrt{3}$ cm² D、2 $\sqrt{3}$ cm²

查看试题解析
9. 如图，AB∥CD，∠E=120°，∠F=90°，∠A+∠C的度数是（）

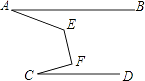A、30° B、35° C、40° D、45°

查看试题解析
10. 如图，△ABC中，∠A=90°，AC= $\frac{\sqrt{7}}{4}$ AB，E是AB边上一点，连结CE，当CE=AB时，AE：EB的值是（）

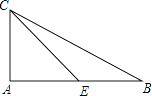A、1 B、2 C、3 D、4

查看试题解析
11. 如图，矩形ABCD，由四块小矩形拼成（四块小矩形放置是既不重叠，也没有空隙），其中②③两块矩形全等，如果要求出①④两块矩形的周长之和，则只要知道（）

A、矩形ABCD的周长 B、矩形②的周长 C、AB的长 D、BC的长

查看试题解析
12. 如图所示的抛物线对称轴是直线x=1，与x轴有两个交点，与y轴交点坐标是（0，3），把它向下平移2个单位后，得到新的抛物线解析式是 y=ax²+bx+c，以下四个结论：
①b²﹣4ac＜0，②abc＜0，③4a+2b+c=1，④a﹣b+c＞0中，判断正确的有（）

A、②③④ B、①②③ C、②③ D、①④

查看试题解析

二、填空题

13. 分解因式：x²﹣9= ．

查看试题解析
14. 在一次60秒跳绳测试中，10名同学跳的次数分别为170，190，180，150，180，180，160，200，180，190，则这次测试所跳次数的众数为

查看试题解析
15. 计算：|﹣5|+（3﹣π）⁰﹣6×3^﹣¹+ $\frac{2}{\sqrt{3} - 1}$ ﹣2sin60°= ．

查看试题解析
16. 如图，直线l切⊙O于点A，点B是l上的点，连结BO并延长，交⊙O于点C，连结AC，若∠C=25°，则∠ABC等于°．

查看试题解析
17. 如图，点A是双曲线y= $\frac{k}{x}$ （x＞0）上的一点，连结OA，在线段OA上取一点B，作BC⊥x轴于点C，以BC的中点为对称中心，作点O的中心对称点O′，当O′落在这条双曲线上时， $\frac{O B}{O A}$ = ．

查看试题解析
18. 如图，已知平面直角坐标系内，A（﹣1，0），B（3，0），点D是线段AB上任意一点（点D不与A，B重合），过点D作AB的垂线l．点C是l上一点，且∠ACB是锐角，连结AC，BC，作AE⊥BC于点E，交CD于点H，连结BH，设△ABC面积为S₁ ， △ABH面积为S₂ ，则S₁•S₂的最大值是．

查看试题解析

三、解答题

19. 先化简，再求值：（ $\frac{2}{a - 1} + 1$ ）÷ $\frac{a^{2} + a}{a^{2} - 2 a + 1}$ ，其中a=3．

查看试题解析
20. 某校社团活动开设的体育选修课有：篮球（A），足球（B），排球（C），羽毛球（D），乒乓球（E），每个学生选修其中的一门，学校对某班全班同学的选课情况进行调查统计后制成了以下两个统计图．

(1)、请你求出该班的总人数，并补全频数分布直方图；

(2)、该班的其中某4个同学，1人选修篮球（A），2人选修足球（B），1人选修排球（C）．若要从这4人中选2人，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．

查看试题解析
21. 如图，一次函数y₁=x﹣2的图象与反比例函数y₂= $\frac{k}{x}$ 的图象相交于A，B两点，与x轴相交于点C．已知tan∠BOC= $\frac{1}{2}$ ，点B的坐标为（m，n），求反比例函数的解析式．

查看试题解析
22. 如图，在平行四边形ABCD中，对角线AC，BD并于点O，经过点O的直线交AB于E，交CD于F．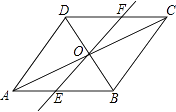

(1)、求证：OE=OF．

(2)、连接DE，BF，则EF与BD满足什么条件时，四边形DEBF是矩形？请说明理由．

查看试题解析
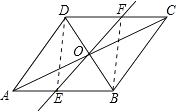23. 如图，已知边长为6的等边△ABC内接于⊙O．

(1)、求⊙O半径；

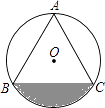(2)、求 $\hat{B C}$ 的长和弓形BC的面积．

查看试题解析
24. 某校为美化校园，计划对面积为1800m²的区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400m²区域的绿化时，甲队比乙队少用4天．

(1)、求甲、乙两工程队每天能完成绿化的面积分别是多少m²？

(2)、若学校每天需付给甲队的绿化费用为0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？

查看试题解析
25. 如图1，对△ABC，D是BC边上一点，连结AD，当 $\frac{A B^{2}}{A C^{2}}$ = $\frac{B D}{C D}$ 时，称AD为BC边上的“平方比线”．同理AB和AC边上也存在类似的“平方比线”．

(1)、如图2，△ABC中，∠BAC=RT∠，AD⊥BC于D．
证明：AD为BC边上的“平方比线”；

(2)、如图3，在平面直角坐标系中，B（﹣4，0），C（1，0），在y轴的正半轴上找一点A，使OA是△ABC中BC边上的“平方比线”．
①求出点A的坐标；
②如图4，以M（ $\frac{8}{3}$ ，0）为圆心，MA为半径作圆，在⊙M上任取一点P（与x轴交点除外）吗，连结PB，PC，PO．求证：PO始终是△PBC中BC边上的“平方比线”．

查看试题解析