2016年浙江省金华市义乌市中考数学模拟试卷

试卷更新日期：2017-01-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 2016的倒数是（）

A、2016 B、﹣2016 C、 $\frac{1}{2016}$ D、﹣ $\frac{1}{2016}$

查看试题解析
2. 宁波轨道交通3号线于2014年12月23日开工建设，预计2020年全线开通，3号线全长32.83千米，32.83千米用科学记数法表示为（　　）

A、3.283×10⁴米 B、32.83×10⁴米 C、3.283×10⁵米 D、3.283×10³米

查看试题解析
3. 下列运算正确的是（）

A、2x+3y=5xy B、a³﹣a²=a C、a﹣（a﹣b）=﹣b D、（a﹣1）（a+2）=a²+a﹣2

查看试题解析
4. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 下列说法正确的是（）

A、两名同学5次成绩的平均分相同，则方差较大的同学成绩更稳定 B、某班选出两名同学参加校演讲比赛，结果一定是一名男生和一名女生 C、学校气象小组预报明天下雨的概率为0.8，则明天下雨的可能性较大 D、为了解我是学校“阳光体育”活动开展情况，必须采用普查的方式

查看试题解析
6.
在市委市政府的领导下，经过全市人民的努力，义乌市获“全国文明城市”提名，为此小兵特制了一个正方体玩具，其展开图如图所示，正方体中与“全”字所在的面正对面上标的字是（）

A、文 B、明 C、城 D、国

查看试题解析
7. 如果一个正比例函数的图象经过不同象限的两点A（2，m），B（n，3），那么一定有（）

A、m＞0，n＞0 B、m＞0，n＜0 C、m＜0，n＞0 D、m＜0，n＜0

查看试题解析
8. 如图，▱ABCD中，AB=3cm，AD=6cm，∠ADC的角平分线DE交BC于点E，交AC于点F，CG⊥DE，垂足为G，DG= $\frac{3}{2} \sqrt{3}$ cm，则EF的长为（）

A、2cm B、 $\sqrt{3}$ cm C、1cm D、 $\frac{3}{2} \sqrt{3}$ cm

查看试题解析
9. 如图，用四个螺丝将四条不可弯曲的木条围成一个木框（形状不限），不计螺丝大小，其中相邻两螺丝的距离依次为3、4、5、7，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任意两个螺丝间的距离的最大值为（）

A、6 B、7 C、8 D、9

查看试题解析
10. 已知二次函数y=x²﹣2x﹣3，点P在该函数的图象上，点P到x轴、y轴的距离分别为d₁、d₂ ．设d=d₁+d₂ ，下列结论中：
①d没有最大值；
②d没有最小值；
③﹣1＜x＜3时，d随x的增大而增大；
④满足d=5的点P有四个．
其中正确结论的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{x - 1}$ 有意义，则x的取值范围是．

查看试题解析
12. 如图，一束平行太阳光照射到正五边形上，若∠1=46°，则∠2= ．

查看试题解析
13. 袋子中装有3个红球、5个黄球、2个白球，这些球的形状、大小、质地等完全相同，随机地从袋子中摸出一个红球的概率是．

查看试题解析
14. 如图，在△ABC中，AB=4，将△ABC绕点B按逆时针方向旋转30°后得到△A₁BC₁ ，则阴影部分的面积为

查看试题解析
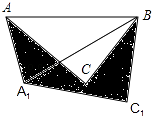15.
如图，点A在双曲线y= $\frac{k}{x}$ 的第一象限的那一支上，AB垂直于y轴于点B，点C在x轴正半轴上，且OC=2AB，点E在线段AC上，且AE=3EC，点D为OB的中点，若△ADE的面积为3，则k的值为．

查看试题解析
16. 如图，点P（t，0）（t＞0）是x轴正半轴上的一点，是以原点为圆心，半径为1的 $\frac{1}{4}$ 圆，且A（﹣1，0），B（0，1），点M是 $\hat{A B}$ 上的一个动点，连结PM，作直角△MPM₁ ，并使得∠MPM₁=90°，∠PMM₁=60°，我们称点M₁为点M的对应点．

(1)、设点A和点B的对应点为A₁和B₁ ，当t=1时，求A₁的坐标；B₁的坐标．

(2)、当P是x轴正半轴上的任意一点时，点M从点A运动至点B，求M₁的运动路径长．

查看试题解析

三、解答题

17. 计算下面各题

(1)、计算：（ $\frac{1}{3}$ ）^﹣¹﹣|﹣2|+ $\sqrt{16}$ ﹣（ $\sqrt{3}$ +1）⁰；

(2)、化简： $\frac{a b + c}{a + b} + \frac{a^{2} - c}{a + b}$ ．

查看试题解析
18. 解方程

(1)、解方程： $\frac{x}{x - 1} + \frac{2}{1 - x} = 3$

(2)、解不等式组： ${\begin{matrix} x - 7 < 4 x + 2 \\ 5 - 2 x < 15 - 4 x \end{matrix}$ ．

查看试题解析
19. 如图，已知E、F分别是▱ABCD的边BC、AD上的点，且BE=DF．

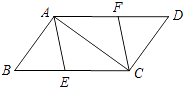(1)、求证：四边形AECF是平行四边形；

(2)、若四边形AECF是菱形，且BC=10，∠BAC=90°，求BE的长．

查看试题解析
20. 成都市某校在推进新课改的过程中，开设的体育选修课有：A﹣篮球，B﹣足球，C﹣排球，D﹣羽毛球，E﹣乒乓球，学生可根据自己的爱好选修一门，学校王老师对某班全班同学的选课情况进行调查统计，制成了两幅不完整的统计图（如图）．

(1)、求出该班的总人数，并补全频数分布直方图；

(2)、求出“足球”在扇形的圆心角是多少度；

(3)、该班班委4人中，1人选修篮球，2人选修足球，1人选修排球，李老师要从这4人中人任选2人了解他们对体育选课的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．

查看试题解析
21. 图1是一个小朋友玩“滚铁环”的游戏，铁环是圆形的，铁环向前滚动时，铁环钩保持与铁环相切．将这个游戏抽象为数学问题，如图2．已知铁环的半径为25cm，设铁环中心为O，铁环钩与铁环相切点为M，铁环与地面接触点为A，∠MOA=α，且sinα= $\frac{3}{5}$ ．

(1)、求点M离地面AC的高度BM；

(2)、设人站立点C与点A的水平距离AC=55cm，求铁环钩MF的长度．

查看试题解析
22. 为进一步缓解城市交通压力，义乌市政府推出公共自行车，公共自行车在任何一个网店都能实现通租通还，某校学生小明统计了周六校门口停车网点各时段的借、还自行车数，以及停车点整点时刻的自行车总数（称为存量）情况，表格中x=1时的y的值表示8：00点时的存量，x=2时的y值表示9：00点时的存量…以此类推，他发现存量y（辆）与x（x为整数）满足如图所示的一个二次函数关系．
时段
x
还车数
借车数
存量y
7：00﹣8：00
1
7
5
15
8：00﹣9：00
2
8
7
n
…
…
…
…
…
根据所给图表信息，解决下列问题：

(1)、m= ，解释m的实际意义：；

(2)、求整点时刻的自行车存量y与x之间满足的二次函数关系式；

(3)、已知10：00﹣11：00这个时段的借车数比还车数的一半还要多2，求此时段的借车数．

查看试题解析
23. 如图1，新定义：直线l₁、l、l₂ ，相交于点O，长为m的线段AB在直线l₂上，点P是直线l₁上一点，点Q是直线l上一点．若∠AQB=2∠APB，则我们称点P是点Q的伴侣点；

(1)、如图1，直线l₂、l的夹角为30°，线段AB在点O右侧，且OA=1，m=2，若要使得∠APB=45°且满足点P是点Q的伴侣点，则OQ=

(2)、如图2，若直线l₁、l₂的夹角为60°，且m=3，若要使得∠APB=30°，线段AB在直线l₂上左右移动．
①当OA的长为多少时，符合条件的伴侣点P有且只有一个？请说明理由；
②是否存在符合条件的伴侣点P有三个的情况？若存在，请直接写出OA长；若不存在，请说明理由．

查看试题解析
24.
如图1，点A，B分别是二次函数y=2x²的图象上的两个点，A、B的横坐标分别为a，b（a＜0，b＞0），点P（0，t）是抛物线对称轴上的任意一点．

(1)、当a+b=0时，探究是否存在t，使得△PAB是以AB为底的等腰三角形？若存在，请直接写出t、a、b的其中一组值；若不存在，请说明理由；

(2)、当a+b≠0时，探究是否存在t，使得△PAB是以AB为底的等腰三角形？若存在，请写出t的取值范围，并用含t的代数式表示a²+b²的值；若不存在，请说明理由；

(3)、
如图2作边长为4的正方形ACDE（A、C、D、E按逆时针排列），使得AC∥x轴，若边CD与二次函数的图象总有交点，求a的取值范围．

查看试题解析

时段	x	还车数	借车数	存量y
7：00﹣8：00	1	7	5	15
8：00﹣9：00	2	8	7	n
…	…	…	…	…