2016年浙江省嘉兴市嘉善县中考数学模拟试卷（3月份）

试卷更新日期：2017-01-19 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的相反数是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 下列汽车标志中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 羊年除夕当日微信红包收发总量达80.8亿个．其中80.8亿用科学记数法可表示为（）

A、8.08×10⁸ B、0.808×10⁹ C、8.08×10⁹ D、0.808×10¹⁰

查看试题解析
4. 下列运算正确的是（）

A、x²+x=x³ B、2x²﹣x²=1 C、x²•x=2x² D、x⁶÷x³=x³

查看试题解析
5. 如图，已知直线a∥b，∠1=75°，∠2=35°，则∠3的度数是（）

A、35° B、40° C、55° D、75°

查看试题解析
6. 抛物线y=ax²+bx+c的图象向左平移5个单位或向右平移1个单位后都会经过原点，则此抛物线的对称轴与x轴的交点的横坐标是（）

A、2 B、﹣2 C、3 D、﹣3

查看试题解析
7. 如图，AB是⊙O的弦，点C在圆上，已知∠OBA=40°，则∠C=（）

A、40° B、50° C、60° D、80°

查看试题解析
8. 如图，直线y₁= $\frac{1}{2}$ x+2与双曲线y₂= $\frac{6}{x}$ 交于A（2，m）、B（﹣6，n）两点．则当y₁＜y₂时，x的取值范围是（）

A、x＞﹣6或0＜x＜2 B、﹣6＜x＜0或x＞2 C、x＜﹣6或0＜x＜2 D、﹣6＜x＜2

查看试题解析
9. 如图，在直角坐标系xOy中，A（﹣4，0），B（0，2），连结AB并延长到C，连结CO，若△COB∽△CAO，则点C的坐标为（）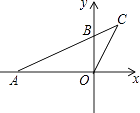

A、（1， $\frac{5}{2}$ ） B、（ $\frac{4}{3}$ ， $\frac{8}{3}$ ） C、（ $\sqrt{5}$ ，2 $\sqrt{5}$ ） D、（ $\sqrt{3}$ ，2 $\sqrt{3}$ ）

查看试题解析
10.
如图，对正方形纸片ABCD进行如下操作：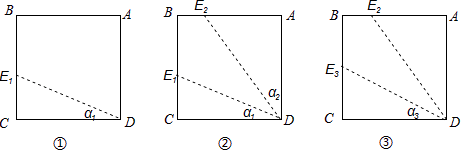
（I）过点D任作一条直线与BC边相交于点E₁（如图①），记∠CDE₁=a₁；
（II）作∠ADE₁的平分线交AB边于点E₂（如图②），记∠ADE₂=a₂；
（III）作∠CDE₂的平分线交BC边于点E₃（如图③），记∠CDE₃=a₃；
按此作法从操作（2）起重复以上步骤，得到a₁ ， a₂ ， …，a_n ， …，现有如下结论：
①当a₁=10°时，a₂=40°；
②2a₄+a₃=90°；
③当a₅=30°时，△CDE₉≌△ADE₁₀；
④当a₁=45°时，BE₂= $\sqrt{2}$ AE₂ ．
其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 分解因式：x²﹣x= ．

查看试题解析
12. 数轴上所表示的关于x的不等式组的解集为

查看试题解析
13. 从长度分别为1、3、5、7的四条线段中任选三条作边，能构成三角形的概率为

查看试题解析
14. 如图，由五个小正方体组成的几何体中，若每个小正方体的棱长都是1，则该几何体的主视图和左视图的面积之和是．

查看试题解析
15. 如图，在△ABC中，AB=2，BC=4，∠B=45°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为．

查看试题解析
16. 如图，⊙O是△ABC的外接圆，BC是⊙O的直径，AB=AC，∠ABC的平分线交AC于点D，交⊙O于点E，连结CE．若CE= $\sqrt{2}$ ，则BD的值为

查看试题解析

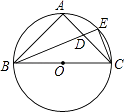
三、解答题

17. 计算下列各题

(1)、计算： $\sqrt{12}$ +2^﹣¹+|﹣ $\frac{1}{2}$ |

(2)、化简：（a﹣3）²+3a（a+2）

查看试题解析
18. 解方程： $\frac{1}{x}$ ﹣ $\frac{x - 1}{2 x}$ =1．

查看试题解析
19. 如图，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A（1，1），B（4，0），C（4，4）．

(1)、按下列要求作图：
①将△ABC向左平移4个单位，得到△A₁B₁C₁；
②将△A₁B₁C₁绕点B₁逆时针旋转90°，得到△A₂B₂C₂ ．

(2)、求点C₁在旋转过程中所经过的路径长．

查看试题解析
20.
随着互联网、移动终端的迅速发展，数字化阅读越来越普及，公交上的“低头族”越来越多．某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查（如图1），并将调查结果绘制成图2和图3所示的统计图（均不完整）．

请根据统计图中提供的信息，解答下列问题：

(1)、求出本次接受调查的总人数，并将条形统计图补充完整；

(2)、表示观点B的扇形的圆心角度数为度；

(3)、若嘉善人口总数约为60万，请根据图中信息，估计嘉善市民认同观点D的人数．

查看试题解析
21. 如图，已知抛物线y=x²+bx+c经过A（﹣1，0）、B（3，0）两点．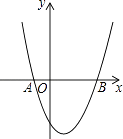

(1)、求抛物线的解析式和顶点坐标；

(2)、当0＜x＜3时，求y的取值范围；

(3)、点P为抛物线上一点，若S_△_PAB=10，求出此时点P的坐标．

查看试题解析
22. 按照有关规定：距高铁轨道 200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物．
如图是一个小区平面示意图，矩形ABEF为一新建小区，直线MN为高铁轨道，C、D是直线MN上的两点，点C、A、B在一直线上，且DA⊥CA，∠ACD=30°．小王看中了①号楼A单元的一套住宅，与售楼人员的对话如下：

(1)、小王心中一算，发现售楼人员的话不可信，请你用所学的数学知识说明理由；

(2)、若一列长度为228米的高铁以252千米/小时的速度通过时，则A单元用户受到影响时间有多长？
（温馨提示： $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7， $\sqrt{37}$ ≈6.1）

查看试题解析
23. 菱形ABCD中，对角线AC、BD交于点O，且AC=2BD，以AD为斜边在菱形ABCD同侧作Rt△ADE．

(1)、
如图1，当点E落在边AB上时．
①求证：∠BDE=∠BAO；
②求 $\frac{D O}{O F}$ 的值；
③当AF=6时，求DF的长．

(2)、
如图2，当点E落在菱形ABCD内部，且AE=DE时，猜想OE与OB的数量关系并证明．

查看试题解析
24. 甲从M地骑摩托车匀速前往N地，同时乙从N地沿同一条公路骑自行车匀速前往M地，甲到达N地后，原路原速返回，追上乙后返回到M地．设甲、乙与N地的距离分别为y₁、y₂千米，甲与乙之间的距离为s千米，设乙行走的时间为x小时．y₁、y₂与x之间的函数图象如图1．

(1)、分别求出y₁、y₂与x的函数表达式；

(2)、求s与x的函数表达式，并在图2中画出函数图象；

(3)、当两人之间的距离不超过5千米时，能够用无线对讲机保持联系．并且规定：持续联系时间不少于15分钟为有效联系时间．求当两人用无线对讲机保持有效联系时，x的取值范围．

查看试题解析