2016年浙江省嘉兴市海宁市中考数学一模试卷

试卷更新日期：2017-01-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数是负数的是（）

A、0 B、﹣1 C、 $\frac{1}{3}$ D、2.5

查看试题解析
2. 初步测算，2015年海宁市全年实现地区生产总值700.23亿元，比上年增长6.7%．其中700.23亿用科学记数法表示为（）

A、700.23×10⁸ B、70.023×10⁹ C、7.0023×10¹⁰ D、7.0023×10⁹

查看试题解析
3. 若分式 $\frac{x - 1}{x - 2}$ 的值为0，则x的值为（）

A、1或2 B、2 C、1 D、0

查看试题解析
4. 如图，在边长为1的小正方形组成的网格中，点A、B、O为格点，则tan∠AOB=（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{3}$ C、 $\frac{\sqrt{10}}{5}$ D、 $\frac{\sqrt{5}}{3}$

查看试题解析
5. 中学生骑电动车上学给交通安全带来隐患，为了解某中学2500个学生家长对“中学生骑电动车上学”的态度，从中随机调查400个家长，结果有360个家长持反对态度，则下列说法正确的是（）

A、调查方式是全面调查 B、样本容量是360 C、该校只有360个家长持反对态度 D、该校约有90%的家长持反对态度

查看试题解析
6. 不等式组 ${\begin{matrix} x \geq - 2 \\ x < 1 \end{matrix}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
7. 如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于 $\frac{1}{2}$ AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（）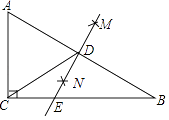

A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC

查看试题解析
8. 如图，在平面直角坐标系中，点A₁、A₂、A₃ ， …是x轴正半轴上的点，且OA₁=A₁A₂=A₂A₃=…，分别过点A₁、A₂、A₃ ， …作y轴的平行线，交反比例函数y= $\frac{6}{x}$ （x＞0）的图象于点B₁、B₂、B₃ ， …，则△A_nB_nB_n₊₁的面积等于（）

A、 $\frac{3}{n}$ B、 $\frac{6}{n}$ C、 $\frac{3}{n + 1}$ D、 $\frac{6}{n + 1}$

查看试题解析
9. 在平面直角坐标系式xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：若y′= ${\begin{matrix} y (x < 0) \\ - y (x \geq 0) \end{matrix}$ ，则称点Q为点P的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．若点P在函数y=﹣x²+2x+3的图象上，则其“可控变点”Q的纵坐标y′关于x的函数图象大致正确的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

10. 因式分解：1﹣x²= ．

查看试题解析
11. 已知方程组 ${\begin{matrix} x + 2 y = 7 \\ 2 x + y = 8 \end{matrix}$ ，则x+y= ．

查看试题解析
12. 在一个不透明的纸箱内放有除颜色外无其他差别的2个红球，8个黄球和10个白球，从中随机摸出一个球为黄球的概率是．

查看试题解析
13. 设n为整数，且n＜ $\sqrt{20}$ ＜n+1，则n= ．

查看试题解析
14. 如图，AB是半圆的直径，点D是 $\hat{B C}$ 的中点，且AB=4，∠BAC=50°，则AD的长度为 cm（结果保留π）．

查看试题解析
15.
如图，在平面直角坐标系xOy中，已知点A（﹣1，0），B（﹣1，1），C（1，0），D（1，2），点P是坐标系内一点，给出定义：若存在过点P的直线l与线段AB，CD都有公共点，则称点P是线段AB，CD的“联络点”．现有点P（x，y）在直线y= $\frac{1}{6}$ x上，且它是线段AB，CD的“联络点”，则x的取值范围是．

查看试题解析

三、简答题

16. 计算下列各题

(1)、计算： $\sqrt{9}$ +cos60°×（ $\frac{1}{2}$ ）^﹣²

(2)、计算： $\frac{x}{x + 1}$ + $\frac{x + 2}{x + 1}$ ．

查看试题解析
17. 已知：如图，AD是△ABC的高，E是AD上一点，AD=BD，DE=DC．

(1)、求证：∠1=∠C．

(2)、当BD=3，DC=1时，求AC的长．

查看试题解析
18. 某市为了了解高峰时段16路车从总站乘该路车出行的人数，随机抽查了10个班次乘该路车人数，结果如下：
14，23，16，25，23，28，26，27，23，25

(1)、这组数据的众数为，中位数为；

(2)、计算这10个班次乘车人数的平均数；

(3)、如果16路车在高峰时段从总站共出车60个班次，根据上面的计算结果，估计在高峰时段从总站乘该路车出行的乘客共有多少？

查看试题解析
19. 如图所示，已知AD∥EF∥BC，FG∥CH，且DF=2CF．

(1)、求AE：BE的值．

(2)、当CH=6时，求FG的长．

查看试题解析
20. 如图是某学校主楼梯从底楼到二楼的楼梯截面图，已知BC=7米，AB=6+3 $\sqrt{3}$ 米，中间平台DE与地面AB平行，且DE的长度为2米，DM、EN为平台的两根支柱，DM、EN垂直于AB，垂足分别为M、N，∠EAB=30°，∠CDF=45°，楼梯宽度为3米．

(1)、若要在楼梯上（包括平台DE）铺满地毯，求地毯的长度；

(2)、沿楼梯从A点到E点铺设价格为每平方米100元的地毯，从E点到C点铺设价格为每平方米120元的地毯，求用地毯铺满整个楼梯共需要花费多少元钱？

查看试题解析
21. 如图，△ABC中，AB=AC，以AB为直径作⊙O，分别交AC，BC于点D，E．

(1)、求证：BE=CE．

(2)、求∠BAC=40°时，∠ADE的度数．

(3)、过点E作⊙O的切线，交AB的延长线于点F，当AO=EF=2时，求图中阴影部分的面积．

查看试题解析
22. 某文具店经销甲、乙两种不同的笔记本，已知两种笔记本的进价之和为10元，每个笔记本的利润均为1元，小王同学买4本甲种笔记本和3本乙种笔记本共用了43元．

(1)、甲、乙两种笔记本的进价分别是多少元？

(2)、该文具店购入这两种笔记本共1000本，花费不超过5200元，则购入甲种笔记本最多多少本？

(3)、店主经统计发现平均每天可售出甲种笔记本300本和乙种笔记本150本．如果两种笔记本的售价各提高1元，则每天将少售出50本甲种笔记本和40本乙种笔记本．为使每天获取的利润更多，店主决定把两种笔记本的价格都提高x元，在不考虑其他因素的条件下，当x定为多少时，才能使该文具店每天销售甲、乙笔记本获取的利润最大？

查看试题解析
23.
如图，在平面直角坐标系中，四边形OABC是矩形，其中点A在x轴的正半轴上，点B的坐标为（4，2），点D为对角线OB上一个动点（不包括端点），∠BCD的平分线交OB于点E．

(1)、求线段OB所在直线的函数表达式，并写出CD的取值范围．

(2)、当∠BCD的平分线经过点A时，求点D的坐标．

(3)、点P是线段BC上的一个动点，求CD十DP的最小值．

查看试题解析