2016年云南省楚雄州双柏县中考数学二模试卷
试卷更新日期：2017-01-19 类型：中考模拟
一、填空题
-
1. ﹣5的倒数是 ．2. 计算：（﹣1）2016+（3.14﹣π）0= ．3. 函数 中自变量x的取值范围是 ．4. 《云南省“十三五”规划纲要》中指出：到2020年，昆明中心城市人口达到400万人左右．将400万用科学记数法表示为 ．5. 已知扇形的半径为3，扇形的圆心角是120°，则该扇形面积为 ．6. 我们把分子为1的分数叫做单位分数．如 ， ， …，任何一个单位分数都可以拆成两个不同的单位分数的和，如 = + ， = + ， = + ，…，根据对上述式子的观察，请你写出 = ．
二、选择题
-
7. 下列运算正确的是（ ）A、a4÷a2=a2 B、（a+b）（a+b）=a2+b2 C、 ﹣ = D、（﹣ ）﹣2=﹣48. 下列四个几何体中，主视图为矩形的是（ ）A、
B、
C、
D、
9. 下列图形中，既是中心对称又是轴对称图形的是（ ）A、等边三角形 B、平行四边形 C、梯形 D、矩形10. 不等式4﹣x≤2（3﹣x）的正整数解有（ ）A、1个 B、2个 C、3个 D、无数个11. 如图，已知：CD∥BE，∠1=68°，那么∠B的度数为（ ）
A、68° B、102° C、110° D、112°12. 在今年“全国助残日”捐款活动中，某班级第一小组7名同学积极捐出自己的零花钱，奉献自己的爱心，他们捐款的数额分别是（单位：元）50、20、50、30、25、50、55，这组数据的众数和中位数分别是（ ）A、50元，30元 B、50元，40元 C、50元，50元 D、55元，50元13. 如图，△ABC是⊙O内接三角形，∠ACB=26°，则∠ABO的度数是（ ）
A、64° B、52° C、54° D、70°14. 已知，函数y= 的图象经过点（﹣1，2），则函数y=kx+2的图象不经过（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限三、解答题
-
15. 先化简，再求值： ，其中x=2．16. 如图，在平行四边形ABCD中，E、F为对角线AC上两点，且AE=CF，请你从图中找出一对全等三角形，并给予证明．
17. 如图，小明在一块平地上测山高，先在B处测得山顶A的仰角为30°，然后向山脚直行100米到达C处，再测得山顶A的仰角为45°，求山高AD是多少？（结果保留整数，测角仪忽略不计，参考数据 ≈1.414， ≈1.73）
18. 昆楚高速公路全长170千米，甲、乙两车同时从昆明、楚雄两地高速路收费站相向匀速开出，经过50分钟相遇，甲车比乙车每小时多行驶10千米．求甲、乙两车的速度．19. 某超市计划在“十周年”庆典当天开展购物抽奖活动，凡当天在该超市购物的顾客，均有一次抽奖的机会，抽奖规则如下：将如图所示的圆形转盘平均分成四个扇形，分别标上1，2，3，4四个数字，抽奖者连续转动转盘两次，当每次转盘停止后指针所指扇形内的数为每次所得的数（若指针指在分界线时重转）；当两次所得数字之和为8时，返现金20元；当两次所得数字之和为7时，返现金15元；当两次所得数字之和为6时返现金10元．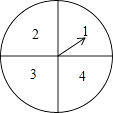
(1)、试用树状图或列表的方法表示出一次抽奖所有可能出现的结果；(2)、某顾客参加一次抽奖，能获得返还现金的概率是多少？20. 某校组织了一次初三科技小制作比赛，有A、B、C、D四个班共提供了100件参赛作品，C班提供的参赛作品的获奖率为50%，其他几个班的参赛作品情况及获奖情况绘制在下列图1和图2两幅尚不完整的统计图中．
(1)、B班参赛作品有多少件？(2)、请你将图2的统计图补充完整；(3)、通过计算说明，哪个班的获奖率高？21. 联通公司手机话费收费有A套餐（月租费15元，通话费每分钟0.1元）和B套餐（月租费0元，通话费每分钟0.15元）两种．设A套餐每月话费为y1（元），B套餐每月话费为y2（元），月通话时间为x分钟．(1)、分别表示出y1与x，y2与x的函数关系式．(2)、月通话时间为多长时，A、B两种套餐收费一样？(3)、什么情况下A套餐更省钱？
