2016年四川省达州市开江县中考数学二模试卷
试卷更新日期:2017-01-19 类型:中考模拟
一、选择题
-
1. 下列各数中,最小的数是( )A、 B、2 C、﹣1 D、﹣2. 净水机的核心部件就是水处理反渗透膜,水处理反渗透膜就像是一个筛子,它的孔径只有0.11纳米,水在压力的作用下一层层过滤,离子以上的杂质像抗生素、重金属、细菌等都能过滤掉,0.11纳米即0.00000000011米,将0.11纳米用科学记数法表示为( )A、1.1×10﹣9米 B、1.1×10﹣10米 C、11×10﹣9米 D、0.11×10﹣9米3. 在一个不透明的盒子中装有3个红球、2个黄球和1个绿球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到黄球的概率为( )A、 B、 C、 D、14. 如图,AF是∠BAC的平分线,EF∥AC交AB于点E.若∠1=25°,则∠BAF的度数为( )
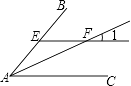 A、15° B、50° C、25° D、12.5°5. 任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)= ,例如18可以分解成1×18,2×9或3×6,则F(18)= ,例如35可以分解成1×35,5×7,则F(35)= ,则F(24)的值是( )A、 B、 C、 D、6. 如图,下边每个大正方形网格,都是由边长为1的小正方形组成,图中阴影部分面积最大的是( )A、
A、15° B、50° C、25° D、12.5°5. 任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)= ,例如18可以分解成1×18,2×9或3×6,则F(18)= ,例如35可以分解成1×35,5×7,则F(35)= ,则F(24)的值是( )A、 B、 C、 D、6. 如图,下边每个大正方形网格,都是由边长为1的小正方形组成,图中阴影部分面积最大的是( )A、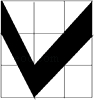 B、
B、 C、
C、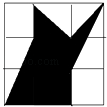 D、
D、 7.
7.“只要人人都献出一点爱,世界将变成美好的人间”.在今年的慈善一日捐活动中,市某中学八年级三班50名学生自发组织献爱心捐款活动.班长将捐款情况进行了统计,并绘制成了统计图.根据如图提供的信息,捐款金额的众数和中位数分别是( )
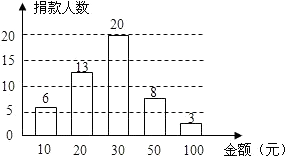 A、20,20 B、30,20 C、30,30 D、20,308. 如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y= (x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )
A、20,20 B、30,20 C、30,30 D、20,308. 如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y= (x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )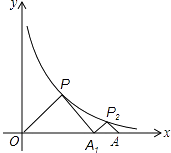 A、(4,0) B、(4 ,0) C、(2,0) D、(2 ,0)9. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,CD=6cm,AD=2cm,动点P、Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到C点停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P点运动的时间为t(s),△BPQ的面积为y(cm2).下图中能正确表示整个运动中y关于t的函数关系的大致图象是( )
A、(4,0) B、(4 ,0) C、(2,0) D、(2 ,0)9. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,CD=6cm,AD=2cm,动点P、Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到C点停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P点运动的时间为t(s),△BPQ的面积为y(cm2).下图中能正确表示整个运动中y关于t的函数关系的大致图象是( )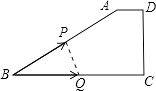 A、
A、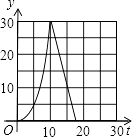 B、
B、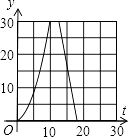 C、
C、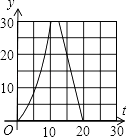 D、
D、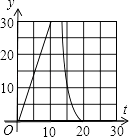 10. 如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③6a﹣b+c<0;④a﹣am2>bm﹣b,且m﹣1≠0,其中正确的说法有( )
10. 如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③6a﹣b+c<0;④a﹣am2>bm﹣b,且m﹣1≠0,其中正确的说法有( )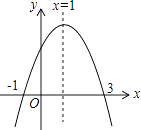 A、①②③ B、②③④ C、①②④ D、②④
A、①②③ B、②③④ C、①②④ D、②④二、填空题
-
11. 在函数y= 中,自变量x的取值范围是 .12. 若m﹣n=2,则2m2﹣4mn+2n2﹣1= .13. 命题“等腰三角形两底角的平分线相等”的逆命题14. 如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为 .
 15. 定义新运算“*”,规则:a*b= ,如1*2=2, * .若x2+x﹣1=0的两根为x1 , x2 , 则x1*x2= .16. 如图,半圆O的直径AB=10cm,D为 上一点,C为 上一点,把弓形沿直线AD翻折,C和直径AB上的点C′重合,若AC=6cm,则AD的长为 .
15. 定义新运算“*”,规则:a*b= ,如1*2=2, * .若x2+x﹣1=0的两根为x1 , x2 , 则x1*x2= .16. 如图,半圆O的直径AB=10cm,D为 上一点,C为 上一点,把弓形沿直线AD翻折,C和直径AB上的点C′重合,若AC=6cm,则AD的长为 .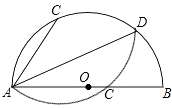
三、解答题
-
17. 计算:( )﹣1×(﹣22) .18. 如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
 19. 先化简,再求值: ,其中x= .20. 李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
19. 先化简,再求值: ,其中x= .20. 李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: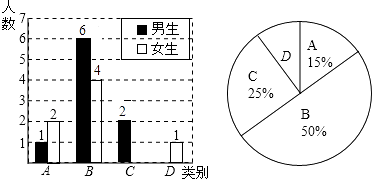 (1)、李老师一共调查了多少名同学?(2)、C类女生有3名,D类男生有1名,将图1条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.21. 某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.(1)、求甲、乙两工程队每天能完成绿化的面积分别是多少m2?(2)、若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?22. 阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1 , y1)与P2(x2 , y2)的“非常距离”,给出如下定义:
(1)、李老师一共调查了多少名同学?(2)、C类女生有3名,D类男生有1名,将图1条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.21. 某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.(1)、求甲、乙两工程队每天能完成绿化的面积分别是多少m2?(2)、若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?22. 阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1 , y1)与P2(x2 , y2)的“非常距离”,给出如下定义:若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
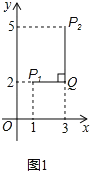 (1)、已知点A(﹣ ,0),B为y轴上的一个动点.
(1)、已知点A(﹣ ,0),B为y轴上的一个动点.①若点B(0,3),则点A与点B的“非常距离”为;
②若点A与点B的“非常距离”为2,则点B的坐标为;
③直接写出点A与点B的“非常距离”的最小值;
(2)、已知点D(0,1),点C是直线y= x+3上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.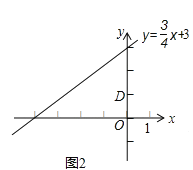 23. 如图,AB是⊙O的直径,BC为⊙O的切线,切点为B,OC平行于AD,OA=2.
23. 如图,AB是⊙O的直径,BC为⊙O的切线,切点为B,OC平行于AD,OA=2.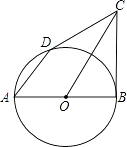 (1)、求证:CD是⊙O的切线;(2)、若AD+OC=9,求CD的长.(结果保留根号)24. 如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC.
(1)、求证:CD是⊙O的切线;(2)、若AD+OC=9,求CD的长.(结果保留根号)24. 如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC.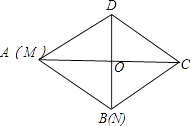 (1)、求证:四边形ABCD是菱形;(2)、如果OA,OB(OA>OB)的长(单位:米)是一元二次方程x2﹣7x+12=0的两根,求AB的长以及菱形ABCD的面积;(3)、若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为 ?25. 如图,抛物线y=ax2+bx+4的图象经过A(﹣3,0),B(5,4),与y轴交于点C.
(1)、求证:四边形ABCD是菱形;(2)、如果OA,OB(OA>OB)的长(单位:米)是一元二次方程x2﹣7x+12=0的两根,求AB的长以及菱形ABCD的面积;(3)、若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为 ?25. 如图,抛物线y=ax2+bx+4的图象经过A(﹣3,0),B(5,4),与y轴交于点C.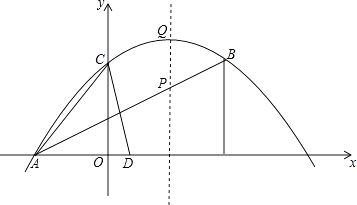 (1)、求抛物线的解析式;(2)、线段AB在第一象限内的部分上有一动点P,过点P作y轴的平行线,交抛物线于点Q,是否存在点P使四边形BPCQ的面积最大?如果存在,请求出点P的坐标及面积的最大值;如果不存在,说明理由;(3)、x轴正半轴上有一点D(1,0),线段AC上是否存在点M,使△AOM∽△ADC?如果存在,直接写出点M的坐标;如果不存在,说明理由.
(1)、求抛物线的解析式;(2)、线段AB在第一象限内的部分上有一动点P,过点P作y轴的平行线,交抛物线于点Q,是否存在点P使四边形BPCQ的面积最大?如果存在,请求出点P的坐标及面积的最大值;如果不存在,说明理由;(3)、x轴正半轴上有一点D(1,0),线段AC上是否存在点M,使△AOM∽△ADC?如果存在,直接写出点M的坐标;如果不存在,说明理由.