2016年山东省济宁市兖州区中考数学二模试卷
试卷更新日期:2017-01-19 类型:中考模拟
一、选择题
-
1. 检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记作负数.从轻重的角度看,最接近标准的工件是( )A、﹣2 B、﹣3 C、3 D、52.
如图是一个正方体纸盒的展开图,其中的六个正方形内分别标有数字“0”、“1”、“2”、“5”和汉字、“数”、“学”,将其围成一个正方体后,则与“5”相对的是( )
 A、0 B、2 C、数 D、学3. 函数y= 中自变量x的取值范围是( )A、x≥﹣3 B、x≠5 C、x≥﹣3或x≠5 D、x≥﹣3且x≠54. 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
A、0 B、2 C、数 D、学3. 函数y= 中自变量x的取值范围是( )A、x≥﹣3 B、x≠5 C、x≥﹣3或x≠5 D、x≥﹣3且x≠54. 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( ) A、800 B、600 C、400 D、2005. 某商品的标价为200元,8折销售仍赚40元,则商品进价为( )元.A、140 B、120 C、160 D、1006.
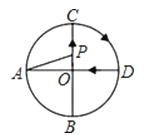
A、800 B、600 C、400 D、2005. 某商品的标价为200元,8折销售仍赚40元,则商品进价为( )元.A、140 B、120 C、160 D、1006.如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
 A、
A、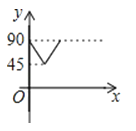 B、
B、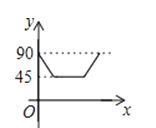 C、
C、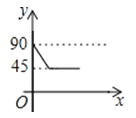 D、
D、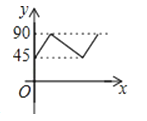 7. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“
7. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( ) A、2a﹣3b B、4a﹣8b C、2a﹣4b D、4a﹣10b8.
A、2a﹣3b B、4a﹣8b C、2a﹣4b D、4a﹣10b8.如图,以点O为圆心的20个同心圆,它们的半径从小到大依次是1、2、3、4、…、20,阴影部分是由第1个圆和第2个圆,第3个圆和第4个圆,…,第19个圆和第20个圆形成的所有圆环,则阴影部分的面积为( )
 A、231π B、210π C、190π D、171π9. 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 , 边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A、231π B、210π C、190π D、171π9. 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 , 边B1C1与CD交于点O,则四边形AB1OD的面积是( ) A、 B、 C、 D、 ﹣110. 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3, ),点C的坐标为( ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
A、 B、 C、 D、 ﹣110. 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3, ),点C的坐标为( ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )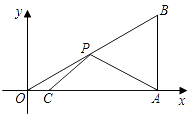 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
11. 如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14cm,则楼高CD为 m.
 12. 甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为 .13. 一三棱锥的三视图如下,这个三棱锥最长棱的长度为 .
12. 甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为 .13. 一三棱锥的三视图如下,这个三棱锥最长棱的长度为 . 14. 如图,在Rt△ABC中,∠ABC=90°,AB=BC= ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是
14. 如图,在Rt△ABC中,∠ABC=90°,AB=BC= ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 15. 如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在边上.
15. 如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在边上.
三、解答题
-
16. 先化简,再求值:( + )÷ ,其中a满足a2﹣4a﹣1=0.17. 某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
 (1)、求本次被调查的学生人数;(2)、补全条形统计图;(3)、该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?18. 如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.
(1)、求本次被调查的学生人数;(2)、补全条形统计图;(3)、该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?18. 如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F. (1)、求证:△AOE≌△COF;(2)、当α=30°时,求线段EF的长度.19. 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.
(1)、求证:△AOE≌△COF;(2)、当α=30°时,求线段EF的长度.19. 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里. (1)、尺规作图:过点P作AB所在直线的垂线,垂足为E(要求:保留作图痕迹,不写作法);(2)、求船P到海岸线MN的距离(即PE的长);(3)、若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)20. 在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= 的一个交点为P(2,m),与x轴、y轴分别交于点A,B.(1)、求m的值;(2)、若PA=2AB,求k的值.21. 阅读下面的材料:
(1)、尺规作图:过点P作AB所在直线的垂线,垂足为E(要求:保留作图痕迹,不写作法);(2)、求船P到海岸线MN的距离(即PE的长);(3)、若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)20. 在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= 的一个交点为P(2,m),与x轴、y轴分别交于点A,B.(1)、求m的值;(2)、若PA=2AB,求k的值.21. 阅读下面的材料:如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1 , x2 ,
① 若x1<x2 , 都有f(x1)<f(x2),则称f(x)是增函数;
②若x1<x2 , 都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)= (x>0)是减函数.
证明:假设x1<x2 , 且x1>0,x2>0
f(x1)﹣f(x2)= ﹣ = =
∵x1<x2 , 且x1>0,x2>0
∴x2﹣x1>0,x1x2>0
∴ >0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)= (x>0)是减函数.
根据以上材料,解答下面的问题:
(1)、函数f(x)= (x>0),f(1)= =1,f(2)= = .计算:f(3)= , f(4)= , 猜想f(x)= (x>0)是函数(填“增”或“减”);
(2)、请仿照材料中的例题证明你的猜想.22. 如图,在平面直角坐标系中,⊙A与x轴相交于C(﹣2,0),D(﹣8,0)两点,与y轴相切于点B(0,4). (1)、求经过B,C,D三点的抛物线的函数表达式;(2)、设抛物线的顶点为E,证明:直线CE与⊙A相切;(3)、在x轴下方的抛物线上,是否存在一点F,使△BDF面积最大,最大值是多少?并求出点F的坐标.
(1)、求经过B,C,D三点的抛物线的函数表达式;(2)、设抛物线的顶点为E,证明:直线CE与⊙A相切;(3)、在x轴下方的抛物线上,是否存在一点F,使△BDF面积最大,最大值是多少?并求出点F的坐标.