2016年江苏省扬州市江都区六校协作联考中考数学二模试卷

试卷更新日期：2017-01-19 类型：中考模拟

进入出卷网下载

一、选择题

1. $\frac{22}{7}$ 是（　　）

A、整数 B、自然数 C、无理数 D、有理数

查看试题解析
2. 下列计算正确的是（）

A、a³+a⁴=a⁷ B、a³•a⁴=a⁷ C、a³﹣a⁴=a^﹣¹ D、a³÷a⁴=a

查看试题解析
3. 有一种病毒呈球形，其最小直径约为0.000 000 08米，用科学记数法表示为（）

A、80×10^﹣⁹米 B、0.8×10^﹣⁷米 C、8×10^﹣⁸米 D、8×10^﹣⁹米

查看试题解析
4. 如图所示的物体的左视图（从左面看得到的视图）是（）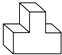

A、 B、 C、 D、

查看试题解析
5. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表．如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加全国数学联赛，那么应选（）
甲
乙
丙
丁
平均数
80
85
85
80
方差
42
42
54
59

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 一个正方形的面积等于10，则它的边长a满足（　　）

A、3＜a＜4 B、5＜a＜6 C、7＜a＜8 D、9＜a＜10

查看试题解析
7. 无论m为何值，点A（m，5﹣2m）不可能在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8.
如图，点A在双曲线y= $\frac{3}{x}$ 上，点B在双曲线y= $\frac{k}{x}$ （k≠0）上，AB∥x轴，过点A作AD⊥x轴于D．连接OB，与AD相交于点C，若AC=2CD，则k的值为（）

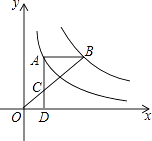A、6 B、9 C、10 D、12

查看试题解析

二、填空题

9. 0的相反数是．

查看试题解析
10. 分解因式：2mx²﹣4mx+2m= ．

查看试题解析
11. 如果分式 $\frac{x^{2} - 4}{x - 2}$ 的值为零，那么x= ．

查看试题解析
12. 如表记录了一名球员在罚球线上投篮的结果．那么，这名球员投篮一次，投中的概率约为（精确到0.1）．
投篮次数（n）
50
100
150
200
250
300
500
投中次数（m）
28
60
78
104
123
152
251
投中频率（m/n）
0.56
0.60
0.52
0.52
0.49
0.51
0.50

查看试题解析
13. 如图，已知AB∥CD∥EF，AD：AF=3：5，BE=12，那么CE的长等于

查看试题解析
14. 一个圆锥的侧面展开图是半径为3，圆心角为120°的扇形，则这个圆锥的高为．

查看试题解析
15.
如图，等腰△ABC中，AB=AC，BC=8．已知重心G到点A的距离为6，则G到点B的距离是．

查看试题解析
16. 如图，正方形ABCD和正方形OEFG中，点A和点F的坐标分别为（3，2），（﹣1，﹣1），则两个正方形的位似中心的坐标是，．

查看试题解析
17. 如图①，在边长为8的等边△ABC中，CD⊥AB，垂足为D，⊙O的圆心与点D重合，⊙O与线段CD交于点E，若将⊙O沿DC方向向上平移1cm后，如图②，⊙O恰与△ABC的边AC，BC相切，则图①中CE的长为 cm．

查看试题解析
18. 若关于x的一元二次方程﹣x²+2ax+2﹣3a=0的一根x₁≥1，另一根x₂≤﹣1，则抛物线y=﹣x²+2ax+2﹣3a的顶点到x轴距离的最小值是．

查看试题解析

三、解答题

19. 计算下列各题

(1)、计算：（ $\sqrt{5}$ ﹣π）⁰﹣6tan30°+（ $\frac{1}{2}$ ）^﹣²+|1+ $\sqrt{3}$ |．

(2)、解不等式组 ${\begin{matrix} 4 (x - 1) \leq 3 (x + 2) \\ \frac{x - 1}{2} < x - 4 \end{matrix}$ ，并写出它的所有整数解．

查看试题解析
20. 先化简，再求值： $\frac{m - 2}{m - 1}$ ÷（1﹣ $\frac{1}{m^{2} - 2 m + 1}$ ），其中m满足一元二次方程m²﹣4m+3=0．

查看试题解析
21. 某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了部分学生的听写结果，绘制成如下的图表．
组别
正常字数x
人数
A
0≤x＜8
10
B
8≤x＜16
15
C
16≤x＜24
25
D
24≤x＜32
m
E
32≤x＜40
n
根据以上信息完成下列问题：

(1)、统计表中的m= ， n= ，并补全条形统计图；

(2)、扇形统计图中“C组”所对应的圆心角的度数是；

(3)、已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数．

查看试题解析
22. 小明有一个呈等腰直角三角形的积木盒，现在积木盒中只剩下如图1所示的九个空格，图2是可供选择的A，B，C，D四块积木．

(1)、小明选择把积木A和B放入图3，要求积木A和B的九个小圆恰好能分别与图3中的九个小圆重合，请在图3中画出他放入方式的示意图（温馨提醒：积木A和B的连接小圆的小线段还是要画上哦！）；

(2)、现从A、B、C、D四块积木中任选两块，请用列表法或画树状图法求恰好能全部不重叠放入的概率

查看试题解析
23. 如图，在▱ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF，PD．

(1)、求证：四边形ABEF是菱形；

(2)、若AB=4，AD=6，∠ABC=60°，求tan∠ADP的值．

查看试题解析
24. “上海迪士尼乐园”将于2016年6月16日开门迎客，小明准备利用暑假从距上海2160千米的某地去“上海迪士尼乐园”参观游览，下图是他在火车站咨询得到的信息：
根据上述信息，求小明乘坐城际直达动车到上海所需的时间．

查看试题解析
25. 如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线，交AB于点E，交CA的延长线于点F．

(1)、求证：EF⊥AB；

(2)、若∠C=30°，EF= $\sqrt{6}$ ，求EB的长．

查看试题解析
26. 在平面直角坐标系xOy中，对于P（a，b）和点Q（a，b′），给出如下定义：若b′= ${\begin{matrix} b (a \geq 1) \\ - b (a < 1) \end{matrix}$ ，则称点Q为点P的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（﹣2，5）的限变点的坐标是（﹣2，﹣5）．

(1)、点（ $\sqrt{3}$ ，1）的限变点的坐标是；

(2)、判断点A（﹣2，﹣1）、B（﹣1，2）中，哪一个点是函数y= $\frac{2}{x}$ 图象上某一个点的限变点？并说明理由；

(3)、若点P（a，b）在函数y=﹣x+3的图象上，其限变点Q（a，b′）的纵坐标的取值范围是﹣6≤b′≤﹣3，求a的取值范围．

查看试题解析
27.
如图，△ABC和△DEF均是边长为4的等边三角形，△DEF的顶点D为△ABC的一边BC的中点，△DEF绕点D旋转，且边DF，DE始终分别交△ABC的边AB，AC于点H，G，图中直线BC两侧的图形关于直线BC成轴对称．连结HH′，HG，GG′，H′G′，其中HH′、GG′分别交BC于点I，J．

(1)、求证：△DHB∽△GDC；

(2)、设CG=x，四边形HH′G′G的面积为y，
①求y关于x的函数解析式和自变量x的取值范围．
②求当x为何值时，y的值最大，最大值为多少？

查看试题解析
28.
已知：如图①，在矩形ABCD中，AB=5，AD= $\frac{20}{3}$ ，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF，BF．

(1)、求AE和BE的长；

(2)、若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB、AD上时，直接写出相应的m的值；

(3)、如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P．与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．

查看试题解析

投篮次数（n）	50	100	150	200	250	300	500
投中次数（m）	28	60	78	104	123	152	251
投中频率（m/n）	0.56	0.60	0.52	0.52	0.49	0.51	0.50

组别	正常字数x	人数
A	0≤x＜8	10
B	8≤x＜16	15
C	16≤x＜24	25
D	24≤x＜32	m
E	32≤x＜40	n

	甲	乙	丙	丁
平均数	80	85	85	80
方差	42	42	54	59