四川省内江市2018年中考数学试卷
试卷更新日期:2018-07-03 类型:中考真卷
一、选择题
-
1. -3的绝对值为( )
A、-3 B、3 C、 D、2. 小时候我们用肥皂水吹泡泡,其泡沫的厚度是约0.000326毫米,用科学记数法表示为( )A、 毫米 B、 毫米 C、 厘米 D、 厘米3. 如图是正方体的表面展开图,则与“前”字相对的字是( ) A、认 B、真 C、复 D、习4. 下列计算正确的是( )A、 B、 C、 D、5. 已知函数 ,则自变量 的取值范围是( )A、 B、 且 C、 D、6. 已知: , 则 的值是( )
A、认 B、真 C、复 D、习4. 下列计算正确的是( )A、 B、 C、 D、5. 已知函数 ,则自变量 的取值范围是( )A、 B、 且 C、 D、6. 已知: , 则 的值是( )
A、 B、 C、3 D、-37. 已知 的半径为 , 的半径为 ,圆心距 ,则 与 的位置关系是( )
A、外离 B、外切 C、相交 D、内切8. 已知 与 相似,且相似比为 ,则 与 的面积比( )A、 B、 C、 D、9. 为了了解内江市2018年中考数学学科各分数段成绩分布情况,从中抽取400名考生的中考数学成绩进行统计分析在这个问题中,样本是指( )A、400 B、被抽取的400名考生 C、被抽取的400名考生的中考数学成绩 D、内江市2018年中考数学成绩10. 在物理实验课上,老师用弹簧秤将铁块悬于盛有水的水槽中,然后匀速向上提起,直到铁块完全露出水面一定高度,则下图能反映弹簧秤的读数 (单位 )与铁块被提起的高度 (单位 )之间的函数关系的大致图象是( )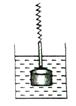 A、
A、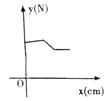 B、
B、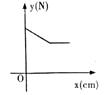 C、
C、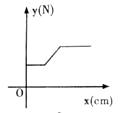 D、
D、 11. 如图,将矩形 沿对角线 折叠,点 落在 处, 交 于点 ,已知 ,则 的度为( )
11. 如图,将矩形 沿对角线 折叠,点 落在 处, 交 于点 ,已知 ,则 的度为( )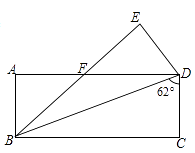 A、 B、 C、 D、12. 如图,在平面直角坐标系中, 的顶点 在第一象限,点 , 的坐标分别为 、 , , ,直线 交 轴于点 ,若 与 关于点 成中心对称,则点 的坐标为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中, 的顶点 在第一象限,点 , 的坐标分别为 、 , , ,直线 交 轴于点 ,若 与 关于点 成中心对称,则点 的坐标为( )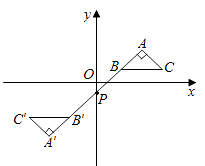 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式: .14. 有五张卡片(形状、大小、质地都相同),正面分别画有下列图形:①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中任取一张,其正面图形既是轴对称图形,又是中心对称图形的概率是 .15. 关于 的一元二次方程 有实数根,则 的取值范围是 .16. 已知, , , , 是反比例函数 图象上四个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形(如图)的边长为半径作四分之一圆周的两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的面积总和是(用含 的代数式表示).

三、解答题
-
17. 计算:18. 如图,已知四边形 是平行四边形,点 、 分别是 、 上的点, ,并且 .

求证:
(1)、(2)、四边形 是菱形19. 为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):组别
成绩分组
频数频率
频数
1
2
0.05
2
4
0.10
3
0.2
4
10
0.25
5
6
6
0.15
合计
40
1.00

根据表中提供的信息解答下列问题:
(1)、频数分布表中的 , , ;(2)、已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 , 72分及以上为及格,预计及格的人数约为 , 及格的百分比约为;(3)、补充完整频数分布直方图.20. 如图是某路灯在铅垂面内的示意图,灯柱 的高为11米,灯杆 与灯柱 的夹角 ,路灯采用锥形灯罩,在地面上的照射区域 长为18米,从 、 两处测得路灯 的仰角分别为 和 ,且 , .求灯杆 的长度. 21. 某商场计划购进 、 两种型号的手机,已知每部 型号手机的进价比每部 型号手机的多500元,每部 型号手机的售价是2500元,每部 型号手机的售价是2100元.
21. 某商场计划购进 、 两种型号的手机,已知每部 型号手机的进价比每部 型号手机的多500元,每部 型号手机的售价是2500元,每部 型号手机的售价是2100元.
(1)、若商场用50000元共购进 型号手机10部, 型号手机20部.求 、 两种型号的手机每部进价各是多少元?
(2)、为了满足市场需求,商场决定用不超过7.5万元采购 、 两种型号的手机共40部,且 型号手机的数量不少于 型号手机数量的2倍.①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
四、填空题
-
22. 已知关于 的方程 的两根为 , ,则方程 的两根之和为.
23. 如图,以 为直径的 的圆心 到直线 的距离 , 的半径 ,直线 不垂直于直线 ,过点 、 分别作直线 的垂线,垂足分别为点 、 ,则四边形 的面积的最大值为. 24. 已知 的三边 、 、 满足 ,则 的外接圆半径.25. 如图,直线 与两坐标轴分别交于 、 两点,将线段 分成 等份,分点分别为 , , ,… ,过每个分点作 轴的垂线分别交直线 于点 , , ,… ,用 , , ,…, 分别表示 , ,…, 的面积,则 .
24. 已知 的三边 、 、 满足 ,则 的外接圆半径.25. 如图,直线 与两坐标轴分别交于 、 两点,将线段 分成 等份,分点分别为 , , ,… ,过每个分点作 轴的垂线分别交直线 于点 , , ,… ,用 , , ,…, 分别表示 , ,…, 的面积,则 .
五、解答题
-
26. 如图,以 的直角边 为直径作 交斜边 于点 ,过圆心 作 ,交 于点 ,连接 .
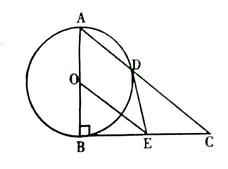 (1)、判断 与 的位置关系并说明理由;(2)、求证: ;(3)、若 , ,求 的长.
(1)、判断 与 的位置关系并说明理由;(2)、求证: ;(3)、若 , ,求 的长.