山东省滨州市阳信县2018届九年级数学中考模拟试卷

试卷更新日期：2018-07-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，负数是（）

A、﹣（﹣5） B、﹣|﹣5| C、（﹣5）² D、﹣（﹣5）³

查看试题解析
2. 如图是五个相同的正方体组成的一个几何体，它的左视图是（）

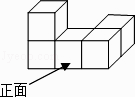A、 B、 C、 D、

查看试题解析
3. 石墨烯是现在世界上最薄的纳米材料，其理论厚度仅是0.00000000034m，这个数用科学记数法表示正确的是（）

A、3.4×10^-9m B、0.34×10^-9m C、3.4×10^-10m D、3.4×10^-11m

查看试题解析
4.
如图，直线AB∥CD，∠C=44°，∠E为直角，则∠1等于（　　）

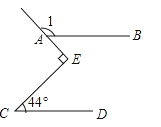A、132° B、134° C、136° D、138°

查看试题解析
5. 下列运算正确的是（）

A、a³+a⁴=a⁷ B、2a³•a⁴=2a⁷ C、（2a⁴）³=8a⁷ D、a⁸÷a²=a⁴

查看试题解析
6. 下面说法正确的有（）
①有理数与数轴上的点一一对应；② $a$ ， $b$ 互为相反数，则 $\frac{a}{b} = - 1$ ；③如果一个数的绝对值是它本身，这个数是正数；④近似数 7.30 所表示的准确数的范围是大于或等于7.295 ，而小于7.305 ．

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
7. 桌面上有A，B两球，若要将B球射向桌面任意一边的黑点，则B球一次反弹后击中A球的概率是（）

A、 $\frac{1}{7}$ B、 $\frac{2}{7}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

查看试题解析
8. 已知a、b、c为常数，点P（a，c）在第二象限，则关于x的方程ax²+bx+c=0根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断

查看试题解析
9. 在“百善孝为先”朗诵比赛中，晓晴根据七位评委所给的某位参赛选手的分数制作了如下表格：
众数
中位数
平均数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
10. 如图，在△ABC中，CA=CB=4，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰好在弧EF上，下列关于图中阴影部分的说法正确的是（）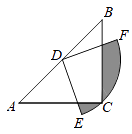

A、面积为 $π - 2$ B、面积为 $\frac{π}{2} - 1$ C、面积为 $2 π - 4$ D、面积随扇形位置的变化而变化

查看试题解析
11. 如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是（）

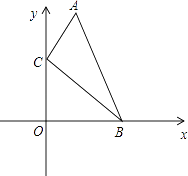A、（0，0） B、（0，1） C、（0，2） D、（0，3）

查看试题解析
12. 如图，在矩形ABCD中，AB=3，BC=4，O为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（）

A、4 B、 $\frac{21}{5}$ C、 $\frac{35}{8}$ D、 $\frac{17}{4}$

查看试题解析

二、填空题

13. 计算：（﹣ $\frac{1}{2}$ ）^﹣³+ $\sqrt{{(\sqrt{2} - 5)}^{2}}$ +2sin45°+（ $\frac{4}{2009 - π}$ ）⁰= ．

查看试题解析
14. 因式分解：x²﹣3x+（x﹣3）= ．

查看试题解析
15. 如图，在平行四边形ABCD中，AE⊥BC，垂足为E，如果AB=5，BC=8， $sin B = \frac{4}{5}$ ，那么EC=.

查看试题解析
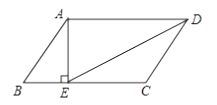16. 如图所示直线y= $\sqrt{3}$ x+ $\sqrt{3}$ 与x轴、y轴分别交于点A、B，当直线绕着点A按顺时针方向旋转到与x轴首次重合时，点B运动到点B₁ ，线段BB₁长度为．

查看试题解析
17. 如图，已知反比例函数y= $\frac{k}{x}$ （x＞0）与正比例函数y=x（x≥0）的图象，点A（1，5）、点A′（5，b）与点B′均在反比例函数的图象上，点B在直线y=x上，四边形AA′B′B是平行四边形，则B点的坐标为．

查看试题解析

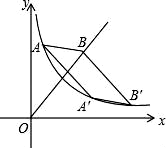
三、解答题

18. 如图，等腰△ABC三个顶点在⊙O上，直径AB=12，P为弧BC上任意一点（不与B，C重合），直线CP交AB延长线与点Q，2∠PAB+∠PDA=90°，下列结论：①若∠PAB=30°，则弧BP的长为 $π$ ；②若PD//BC，则AP平分∠CAB；③若PB=BD，则 $P D = 6 \sqrt{3}$ ，④无论点P在弧 $\vec{B C}$ 上的位置如何变化，CP·CQ为定值. 正确的是.

查看试题解析
19. 先化简，再求值： $(\frac{2 m}{m + 2} - \frac{m}{m - 2}) \div \frac{m}{m^{2} - 4}$ ，再从0，-2，2， $\sqrt{2} + 2$ 中选取一个适当的数代入求值.

查看试题解析
20. 解不等式组： ${\begin{matrix} x + 3 (x - 2) \geq 2 \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$

查看试题解析
21. 列方程解应用题：某景区一景点改造工程要限期完成，甲工程队单独做可提前一天完成，乙工程队单独做要误期6天，现由两工程队合做4天后，余下的由乙工程队独做，正好如期完成，则工程期限是多少天？

查看试题解析
22. 如图：在Rt△ABC中，∠ACB=90°，AB=6，过点C的直线MN∥AB，D为AB上一点，过点D作DE⊥BC，交直线MN于点E，垂足为F，连结CD，BE，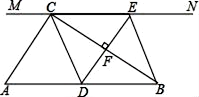

(1)、当点D是AB的中点时，四边形BECD是什么特殊四边形？说明你的理由

(2)、在（1）的条件下，当∠A=时四边形BECD是正方形．

查看试题解析
23. 如图的⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，过点D、A分别作⊙O的切线交于点G，并与AB延长线交于点E．

(1)、求证：∠1=∠2．

(2)、已知：OF：OB=1：3，⊙O的半径为3，求AG的长．

查看试题解析
24. 在平面直角坐标系中，二次函数 $y = a x^{2} + b x + 2$ 的图象与 $x$ 轴交于A（－3，0），B（1，0）两点，与y轴交于点C．

(1)、求这个二次函数的解析式；

(2)、点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP的面积最大？若存在，求出点P的坐标；若不存在，说明理由；

(3)、点Q是直线AC上方的抛物线上一动点，过点Q作QE垂直于 $x$ 轴，垂足为E．是否存在点Q，使以点B、Q、E为顶点的三角形与△AOC相似？若存在，直接写出点Q的坐标；若不存在，说明理由；

查看试题解析

众数	中位数	平均数	方差
8.5	8.3	8.1	0.15