吉林省长春市2018届九年级数学中考模拟试卷（一）

试卷更新日期：2018-07-03 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2的绝对值是（）

A、﹣2 B、﹣ $\frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 据统计，2017年国庆黄金周内旅游市场接待游客约589000000人次.589000000这个数用科学记数法表示为（）

A、589×10⁶ B、58.9×10⁷ C、5.89×10⁸ D、0.589×10⁹

查看试题解析
3. 如图所示的几何体是由五个完全相同的正方体组成的，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 计算（x²y）³的结果是（）

A、x⁶y³ B、x⁵y³ C、x⁵y D、x²y³

查看试题解析
5. 关于x的一元二次方程x²+4x+k=0有两个实数根，则k的取值范围是（）

A、k≤﹣4 B、k≥﹣4 C、k≤4 D、k＞4

查看试题解析
6. 如图，若以平行四边形一边AB为直径的圆恰好与边CD相切于点D，则∠C的度数是（）

A、40° B、45° C、50° D、60°

查看试题解析
7.
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（）

A、（ $\sqrt{3}$ ，﹣1） B、（1，﹣ $\sqrt{3}$ ） C、（ $\sqrt{2}$ ，﹣ $\sqrt{2}$ ） D、（﹣ $\sqrt{2}$ ， $\sqrt{2}$ ）

查看试题解析
8. 如图，在平面直角坐标系中，菱形OABC的顶点B在y轴正半轴上，顶点C在函数y= $\frac{k}{x}$ （x＜0）的图象上．若对角线AC=6，OB=8，则k的值是（）

A、24 B、12 C、﹣12 D、﹣6

查看试题解析

二、填空题

9. 因式分解：y³﹣16y= ．

查看试题解析
10. 不等式组 ${\begin{matrix} x + 2 > 0 \\ 2 x - 1 \leq 0 \end{matrix}$ 的解集是．

查看试题解析
11. 如图，AB∥CD，BE交CD于点D，CE⊥BE于点E，若∠B=34°，则∠C的大小为度．

查看试题解析
12. 如图，AB∥CD∥EF，AF与BE相交于点G，且AG＝2，GD＝1，DF＝5，那么 $\frac{B C}{C E}$ 的值等于．

查看试题解析
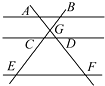13. 如图，以AB为直径，点O为圆心的半圆经过点C，若AC=BC= $\sqrt{2}$ ，则图中阴影部分的面积是

查看试题解析
14. 如图，线段AB的长为4，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE，那么DE长的最小值是．

查看试题解析

三、解答题

15. 先化简，再求值：（2a﹣b）²﹣a（4a﹣3b），其中a=1，b= $\sqrt{3}$ ．

查看试题解析
16. 甲、乙两人做摸球游戏，在不透明的口袋里放入大小相同的两个黑球和两个白球，甲摸出两个球后放回，乙再摸出两个球，若摸出一黑一白甲赢，若摸出两个相同颜色的乙赢．这个游戏公平吗？为什么？

查看试题解析
17. 在大城市，很多上班族选择“低碳出行”，电动车和共享单车成为他们的代步工具．某人去距离家8千米的单位上班，骑共享单车虽然比骑电动车多用20分钟，但却能强身健体，已知他骑电动车的速度是骑共享单车的1.5倍，求骑共享单车从家到单位上班花费的时间．

查看试题解析
18. 为增强学生体质，各学校普遍开展了阳光体育活动，某校为了解全校1000名学生每周课外体育活动时间的情况，随机调查了其中的50名学生，对这50名学生每周课外体育活动时间x（单位：小时）进行了统计．根据所得数据绘制了一幅不完整的统计图，并知道每周课外体育活动时间在6≤x＜8小时的学生人数占24%．根据以上信息及统计图解答下列问题：

(1)、本次调查属于调查，样本容量是；

(2)、请补全频数分布直方图中空缺的部分；

(3)、求这50名学生每周课外体育活动时间的平均数；

(4)、估计全校学生每周课外体育活动时间不少于6小时的人数．

查看试题解析
19. 如图，在▱ABCD中，AB＜BC，以点A为圆心，AB长为半径作圆弧交AD于点F，再分别以点B、F为圆心，大于BF的一半长为半径作圆弧，两弧交于一点P，连结AP并延长交BC于点E，连结EF．

(1)、四边形ABEF是（填“矩形”、“菱形”、“正方形”或“无法确定”）（直接填写结果），并证明你的结论．

(2)、AE、NF相交于点O，若四边形ABEF的周长为40，BF=10，则AE的长为， ∠ADC=°，（直接填写结果）

查看试题解析
20. 在数学活动课上，九年级（1）班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离，现测得亭子A位于点P北偏西30°方向，亭子B位于点P北偏东42°方向，测得点P与亭子A之间的距离为200米，求亭子A与亭子B之间的距离．（结果精确到1米）
【参考数据：sin42°=0.67，cos42°=0.74，tan42°=0.90， $\sqrt{3}$ =1.73】

查看试题解析
21. 周末，甲、乙两名大学生骑自行车去距学校6000米的净月潭公园．两人同时从学校出发，以a米/分的速度匀速行驶．出发4.5分钟时，甲同学发现忘记带学生证，以1.5a米/分的速度按原路返回学校，取完学生证（在学校取学生证所用时间忽略不计），继续以返回时的速度追赶乙．甲追上乙后，两人以相同的速度前往净月潭．乙骑自行车的速度始终不变．设甲、乙两名大学生距学校的路程为s（米），乙同学行驶的时间为t（分），s与t之间的函数图象如图所示．

(1)、求a、b的值．

(2)、求甲追上乙时，距学校的路程．

(3)、当两人相距500米时，直接写出t的值是．

查看试题解析
22. 定义：在三角形中，把一边的中点到这条边的高线的距离叫做这条边的中垂距．
例：如图①，在△ABC中，D为边BC的中点，AE⊥BC于E，则线段DE的长叫做边BC的中垂距．

(1)、设三角形一边的中垂距为d（d≥0）．若d=0，则这样的三角形一定是，推断的数学依据是

(2)、如图②，在△ABC中，∠B=45°，AB= $3 \sqrt{2}$ ，BC=8，AD为边BC的中线，求边BC的中垂距．

(3)、如图③，在矩形ABCD中，AB=6，AD=4．点E为边CD的中点，连结AE并延长交BC的延长线于点F，连结AC．求△ACF中边AF的中垂距．

查看试题解析
23. 如图，在四边形ABCD中，AD∥BC，∠B=90°，射线ED⊥BC于点E，AD=AB=BE= $\frac{1}{2}$ BC=4，动点P从点E出发，沿射线ED以每秒2个单位长度的速度运动，以PE为对角线做正方形PMEN，设运动时间为t秒，正方形PMEN与四边形ABCD重叠部分面积为S．

(1)、当点N落在边DC上时，求t的值．

(2)、求S与t的函数关系式．

(3)、当正方形PMEN被直线BD分成2：1两部分时，直接写出t的值．

查看试题解析
24. 在平面直角坐标系中，规定：抛物线y=a（x﹣h）²+k的关联直线为y=a（x﹣h）+k．
例如：抛物线y=2（x+1）²﹣3的关联直线为y=2（x+1）﹣3，即y=2x﹣1．

(1)、如图，对于抛物线y=﹣（x﹣1）²+3．
①该抛物线的顶点坐标为，关联直线为，该抛物线与其关联直线的交点坐标为和；

(2)、顶点在第一象限的抛物线y=﹣a（x﹣1）²+4a与其关联直线交于点A，B（点A在点B的左侧），与x轴负半轴交于点C，直线AB与x轴交于点D，连结AC、BC．
①求△BCD的面积（用含a的代数式表示）．

查看试题解析