黑龙江省哈尔滨市平房区2018届九年级中考调研测试数学试卷（一）

试卷更新日期：2018-07-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果冰箱冷藏室的温度是5℃，冷冻室的温度是-3℃，则冷藏室比冷冻室高（）

A、8℃ B、-8℃ C、-2℃ D、2℃

查看试题解析
2. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，正确的是（）

A、x·x²= x² B、（xy）²=xy² C、 ${(x^{2})}^{3} = x^{6}$ D、x²+x²=2x⁴

查看试题解析
4. 如左图是由几个相同的小正方体搭成的一个几何体，它的左视图是（）

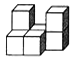A、 B、 C、 D、

查看试题解析
5. 反比例函数 $y = - \frac{k^{2}}{x}$ (k为常数，k≠0)的图象位于（）

A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限

查看试题解析
6. 如图，飞机在空中B处探测到它的正下方地面上目标C，此时飞行高度BC=1200米，从飞机上看地面指挥台A的俯角α的正切值为 $\frac{3}{4}$ 则飞机与指挥台之间AB的距离为（）米

A、1200 B、1600 C、1800 D、2000

查看试题解析
7. 将抛物线 $y = x^{2}$ 向左平移2个单位，再向下平移3个单位，得到的抛物线解析式是( ）

A、 $y = {(x - 2)}^{2} - 3$ B、 $y = {(x - 2)}^{2} + 3$ C、 $y = {(x + 2)}^{2} - 3$ D、 $y = {(x + 2)}^{2} + 3$

查看试题解析
8. 如图，在菱形ABCB中，点E在AD边上，EF∥CD，交对角线BD于点F，则下列结论中错误的是（）

A、 $\frac{D E}{A E} = \frac{D F}{B F}$ B、 $\frac{E F}{A D} = \frac{D F}{D B}$ C、 $\frac{E F}{A D} = \frac{D F}{B F}$ D、 $\frac{E F}{C D} = \frac{D F}{D B}$

查看试题解析
9. 如图，△ABC为等边三角形，将△ABC绕点A逆时针旋转75°，得到△AED，过点E作EF⊥AC，垂足为点F，若AC=8，则AF的长为( ）

A、 $4$ B、3 C、 $4 \sqrt{6}$ D、 $4 \sqrt{2}$

查看试题解析
10. 在一次越野赛中，甲选手匀速跑完全程，乙选手1.5小时后速度为每小时10千米，两选手的行程y(千米)随时间x(小时）变化的图像（全程）如图所示，则乙比甲晚到（）小时.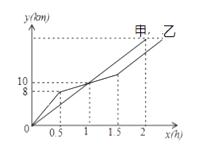

A、0.4 B、0.3 C、0.2 D、0.1

查看试题解析

二、填空题

11. 把384000000用科学记数法表示为.

查看试题解析
12. 函数 $y = \frac{x - 1}{2 x + 6}$ 的自变量 $x$ 的取值范围是.

查看试题解析
13. 计算： $\sqrt{27} - \sqrt{\frac{1}{3}} =$ .

查看试题解析
14. 不等式组 ${\begin{matrix} x - 2 \geq - 1 \\ 3 x - 1 > 8 \end{matrix}$ 的解集为.

查看试题解析
15. 把多项式 $3 a^{3} - 12 a^{2} + 12 a$ 分解因式的结果是.

查看试题解析
16. 分式方程 $\frac{1}{x - 1}$ = $\frac{2}{x}$ 的解是．

查看试题解析
17. 一个扇形的面积为12πcm² ，圆心角为120°，则该扇形的半径是.

查看试题解析
18. 星期一早晨，小红、小丽两人同在新疆大街公交站等车去同一所学校上学，此时恰好有途经该校公交站的三辆车同时进站(不考虑其它因素)，则小红和小丽同乘一辆车的概率为.

查看试题解析
19. 在正方形ABCD中，点0为正方形的中心，直线m经过点0，过A、B两点作直线m的垂线AE、BF，垂足分别为点E、F，若AE=2，BF=5，则EF长为.

查看试题解析
20. 如图，在△ABC中，AC=BC，D为AB的中点，F为BC边上一点，连接CD、AF交干点E.若∠FAC=90°-3∠BAF，BF：AC=2：5，EF=2，则AB长为.

查看试题解析

三、解答题

21. 先化简，再求代数式 $\frac{a}{a + 1} - \frac{a^{2} - 6 a + 9}{a^{2} - 1} \div \frac{a - 3}{a - 1}$ 的值，其中 $a = 3 tan 30^{\circ} - 3 cos 60^{\circ}$ .

查看试题解析
22. 如图，方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。

①在图中画一个以AB为腰的等腰三角形△ABC，点C在小正方形的顶点上，且tan∠B=3；
②在图中画一个以AB为底的等腰三角形△ABD，点D在小正方形的顶点上，且△ABD是锐角三角形.连接CD，请直接写出线段CD的长。

查看试题解析
23. 随着2018年两会的隆重召开，中学校园掀起了关注时事政治的热潮我区及时开展“做一个关心国家大事的中学生”主题活动。为了了解我区中学生获取时事新闻的主要途径，分别从电脑上网、手机上网、听广播、看电视、看报纸五个方面，在全区范围内随机抽取了若干名中学生进行问卷调查(每名中学生只选一种主要途径)，根据调查结果绘制了如图所示的不完整的统计图请根据统计图的信息回答下列问题：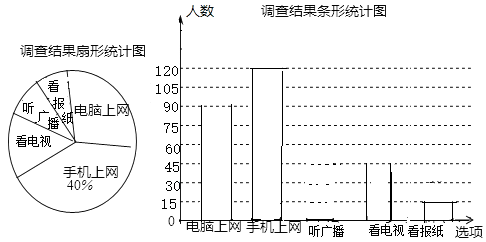

(1)、本次调查共抽取了中学生多少人?

(2)、求本次调查中，以听广播获取时事新闻为主要途径的人数并补全条形统计图；

(3)、若本区共有中学生7000人，请你估计我区以看电视获取时事新闻为主要途径的中学生有多少人？

查看试题解析
24. 已知：如图，AD是△ABC的中线，E为AD的中点，过点A作AF∥BC交BE延长线于点F，连接CF.

(1)、如图1，求证：四边形ADCF是平行四边形；

(2)、如图2.连接CE，在不添加任何助线的情况下，请直接写出图2中所有与△BEC面积相等的三角形。

查看试题解析
25. 平房区政府为了“安全，清激、美丽”河道，计划对何家沟平房区河段进行改造，现有甲乙两个工程队参加改造施工，受条件阻制，每天只能由一个工程队。若甲工程队先单独施工3天，再由乙工程队单独施工5天，则可以完成550米施工任务；若甲工程队先单独施工2天，再由乙工程对单独施工4天，则可以完成420米的施工任务。

(1)、求甲、乙两个工程队平均每天分别能完成多少米施工任务？

(2)、何家沟平房区河段全长6000米。若工期不能超过90天，乙工程队至少施工多少天?

查看试题解析
26. 已知：AB是⊙0直径，C是⊙0外一点，连接BC交⊙0于点D，BD=CD，连接AD、AC.

(1)、如图1，求证：∠BAD=∠CAD

(2)、如图2，过点C作CF⊥AB于点F，交⊙0于点E，延长CF交⊙0于点G.过点作EH⊥AG于点H，交AB于点K，求证AK=2OF；

(3)、如图3，在(2)的条件下，EH交AD于点L，若0K=1，AC=CG，求线段AL的长.

查看试题解析
27. 在平面直角坐标系中，O为坐标原点，抛物线 $y = a x^{2} + b x - 3$ 交x轴于点A(l，0)、B(3，0)，交y轴于点C.

(1)、如图1，求抛物线的解析式；

(2)、如图2，点P为对称轴右侧第四象限抛物线上一点，连接PA并延长交y轴于点K，点P横坐标为t，△PCK的面积为S，求S与t的函数关系式(直接写出自变量t的取值范围）；

(3)、如图3，在(2)的条件下，过点A作AD⊥AP交y轴于点D.连接OP，过点O作OE⊥OP交AD延长线于点E，当OE=OP时，延长EA交抛物线于点Q，点M在直线EC上，连接QM，交AB于点H，将射线QM绕点Q逆时针旋转45°，得到射线QN交AB于点F，交直线EC于点N，若AH：HF=3：5，求 $\frac{S_{△ N M K}}{S}$ 的值.

查看试题解析