黑龙江省哈尔滨市阿城区2018届九年级3月调研数学试卷
试卷更新日期:2018-07-03 类型:中考模拟
一、单选题
-
1. 下列各数中,小于-2的数是( )
A、 B、-π C、-1 D、12. 下列运算中,正确的是( )
A、 B、 C、 D、3. 下列四个图形中既是轴对称图形,又是中心称图形的是( )
A、 B、
B、 C、
C、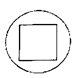 D、
D、 4. 如图是一个由5个相同的正方体组成的立体图形,则它的俯视图为( )
4. 如图是一个由5个相同的正方体组成的立体图形,则它的俯视图为( )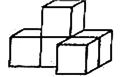 A、
A、 B、
B、 C、
C、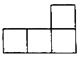 D、
D、 5. 关于二次函数y=-2(x-3) +5的最大值,下列说法正确的是( )A、最大值是3 B、最大值是-3 C、最大值是5 D、最大值是-56. 反比例函数y= 图象上的两个点为( )、( ),且 ,则下列式子一定成立的是( )
5. 关于二次函数y=-2(x-3) +5的最大值,下列说法正确的是( )A、最大值是3 B、最大值是-3 C、最大值是5 D、最大值是-56. 反比例函数y= 图象上的两个点为( )、( ),且 ,则下列式子一定成立的是( )
A、 B、 C、 D、不能确定7. 如图,从热气球C处测得地面A,B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为100m,点A,D,B在同一直线上,CD⊥AB,则A、B两点的距离是( ) A、200m B、200 m C、 m D、8. 如图,点F是▱ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
A、200m B、200 m C、 m D、8. 如图,点F是▱ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( ) A、 B、 C、 D、9. 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A、 B、 C、 D、9. 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( ) A、45° B、50° C、60° D、75°10. 小颖家到学校1200米,其中有一段为上坡路,另一段为下坡路,她去学校共用了16分钟。假设小颖上坡路的平均速度是3千米/时,下坡路的平均速度是5千米/时,若设小颖上坡用了x分钟,下坡用了y分钟。则可列方程组为( )
A、45° B、50° C、60° D、75°10. 小颖家到学校1200米,其中有一段为上坡路,另一段为下坡路,她去学校共用了16分钟。假设小颖上坡路的平均速度是3千米/时,下坡路的平均速度是5千米/时,若设小颖上坡用了x分钟,下坡用了y分钟。则可列方程组为( )
A、 B、 C、 D、二、填空题
-
11. 2018年春节黄金周,哈尔滨太平国际机场运送旅客约430000人次,创历史新高,请将430000用科学记数法表示为.12. 函数y= 中自变量x的取值范围是:.
13. 计算: .
14. 因式分解: .15. 不等式组 的解集是.
16. 一个扇形的弧长是 Cm,半径是6cm,则此扇形的圆心角是度.
17. 若抛物线y=(x-m) +(m+1)的顶点在第一象限,则m的取值范围为.
18. 五张卡片正面分别标有 、0、tan45°、-1、 ,每张卡片的背面完全相同,则随机抽两张卡片都是有理数的概率是.
19. 矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为 .
20. 如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=2 ,则DF=.
三、解答题
-
21. 先化简,再求值: ,其中 .22. 如图网格中每个小正方形的边长均为1,线段AB、CD的端点都在小正方形的顶点上.
(1)、图(1)中,画一个以线段AB一边的四边形ABEF,且四边形ABEF是面积为7的中心对称图形,点E、F都在小正方形的顶点上,并直接写出线段BE的长;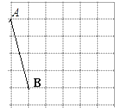 (2)、在图(2)中,画一个以线段CD为斜边直角三角形CDG,且△CDG的面积是2,点G在小方形的顶点上。
(2)、在图(2)中,画一个以线段CD为斜边直角三角形CDG,且△CDG的面积是2,点G在小方形的顶点上。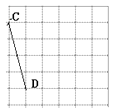 23. 某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:
23. 某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: (1)、本次被调查的学生有名;
(1)、本次被调查的学生有名;
(2)、补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)、该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
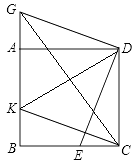
24. 如图,四边形ABCD是正方形,点E、K分别在BC、AB上,CE=BK,点G在BA的延盖长线上,且DG⊥DE.
(1)、如图(1)求证:CK=DG; (2)、如图(2)不添加任何辅助线的条件下,直接写出图中所有的与四边形BEDK面积相等
(2)、如图(2)不添加任何辅助线的条件下,直接写出图中所有的与四边形BEDK面积相等的三角形。
 25. 某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支。
25. 某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支。
(1)、求第一批每支钢笔的进价是多少元?(2)、第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折?
26. 如图,四边形ABCD是⊙O的内接四边形,AB=CD. (1)、如图(1),求证:AD∥BC;
(1)、如图(1),求证:AD∥BC;
(2)、如图(2),点F是AC的中点,弦DG∥AB,交BC于点E,交AC于点M,求证:AE=2DF;(3)、在(2)的条件下,若DG平分∠ADC,GE=5 ,tan∠ADF=4 ,求⊙O的半径。27. 已知:如图,在平面直角坐标系中,直线y=-x+6与x轴、y轴分别交于A、B两点、直线y= ax+a经过点B交x轴于点C.

 (1)、求AC长;(2)、点D为线段BC上一动点,过点D作x轴平行线分别交OB、AB于点E、F,点G为AF中点,直线EG交x轴于H,设点D的横坐标为t,线段AH长为d(d≠0),求d与t之间的函数关系式;
(1)、求AC长;(2)、点D为线段BC上一动点,过点D作x轴平行线分别交OB、AB于点E、F,点G为AF中点,直线EG交x轴于H,设点D的横坐标为t,线段AH长为d(d≠0),求d与t之间的函数关系式;
(3)、在(2)的条件下,点K为线段OA上一点,连接EK,过F作FM⊥EK,直线FM交x轴于点M,当KH=2CO,点0到直线FM的距离为 时,求点D的坐标。