河南省商丘市柘城县2018届数学中考一模试卷
试卷更新日期：2018-07-03 类型：中考模拟
一、单选题
-
1. ﹣ 的绝对值是（ ）A、 B、﹣ C、7 D、﹣72. 据统计，2013年河南省旅游业总收入达到约3875.5亿元．若将3875.5亿用科学记数法表示为3.8755×10n ， 则n等于（ ）A、10 B、11 C、12 D、133.
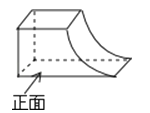
如图所示的几何体的俯视图是（ ）
A、
B、
C、
D、
4. 分式方程 的根为（ ）A、﹣1或3 B、﹣1 C、3 D、1或﹣35. 在一次体育测试中，小芳所在小组8人的成绩分别是：46，47，48，48，49，49，49，50，则这8人体育成绩的中位数和众数分别是（ ）
A、47，46 B、48，47 C、48.5，49 D、49，496. 下列方程是关于x的一元二次方程的是（ ）A、x2+ =1 B、ax2+bx+c=0 C、（x+1）（x+2）=1 D、3x2﹣2xy﹣5y=07. 如图所示，有一张一个角为60°的直角三角形纸片，沿其一条中位线剪开后，不能拼成的四边形是（ ）
A、邻边不等的矩形 B、等腰梯形 C、有一角是锐角的菱形 D、正方形8. 三张外观相同的卡片分别标有数字1、2、3，从中随机一次抽出两张，这两张卡片上的数字恰好都小于3的概率是（ ）A、 B、 C、 D、9. 如图，在Rt△ABC中，∠C=90°，AC=1cm，BC=2cm，点P从点A出发，以1cm/s的速度沿折线AC→CB→BA运动，最终回到点A，设点P的运动时间为x（s），线段AP的长度为y（cm），则能够反映y与x之间函数关系的图象大致是（ ）
A、
B、
C、
D、
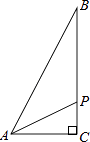10. 如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′，A′C′交AB于点E，若AD=BE，则△A′DE的面积是（ ）
A、3 B、5 C、11 D、6二、填空题
-
11. 计算：（﹣2）0﹣ = ．12. 不等式组 的所有整数解的和为 .
13. 已知点P（a，b）在反比例函数y= 的图象上，若点P关于y轴对称的点在反比例函数y= 的图象上，则k的值为 ．14. 如图，抛物线的顶点为P（﹣2，2），与y轴交于点A（0，3）．若平移该抛物线使其顶点P沿直线移动到点P′（2，﹣2），点A的对应点为A′，则抛物线上PA段扫过的区域（阴影部分）的面积为 ．
15. 如图，矩形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，BE的长为 ．
16. 如图，在Rt△ABC中，∠ABC=90°，点M是AC的中点，以AB为直径作⊙O分别交AC，BM于点D，E.
(1)、求证：MD=ME(2)、填空：①若AB=6，当AD=2DM时，DE=；②连接OD，OE，当∠A的度数为时，四边形ODME是菱形.
三、解答题
-
17. 先化简，再求值：（x+y）2﹣2y（x+y），其中x= ，y= ．
18. 某兴趣小组为了了解本校男生参加课外体育锻炼情况，随机抽取本校300名男生进行了问卷调查，统计整理并绘制了如下两幅尚不完整的统计图．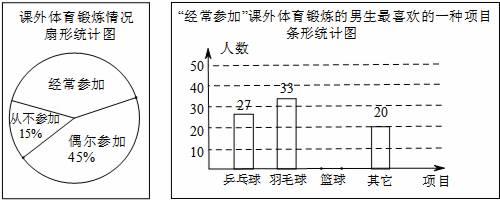
请根据以上信息解答下列问题：
(1)、课外体育锻炼情况扇形统计图中，“经常参加”所对应的圆心角的度数为；
(2)、请补全条形统计图；(3)、该校共有1200名男生，请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数；
(4)、小明认为“全校所有男生中，课外最喜欢参加的运动项目是乒乓球的人数约为1200× =108”，请你判断这种说法是否正确，并说明理由．
19. 如图，山顶建有一座铁塔，塔高BC=80米，测量人员在一个小山坡的P处测得塔的底部B点的仰角为45°，塔顶C点的仰角为60°．已测得小山坡的坡角为30°，坡长MP=40米．求山的高度AB（精确到1米）．（参考数据： ≈1.414， ≈1.732）
20. 如图，在直角梯形OABC中，BC∥AO，∠AOC=90°，点A，B的坐标分别为（5，0），（2，6），点D为AB上一点，且BD=2AD，双曲线y= （k＞0）经过点D，交BC于点E．
(1)、求双曲线的解析式；(2)、求四边形ODBE的面积．21. 某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡：①金卡售价600元/张，每次凭卡不再收费．
②银卡售价150元/张，每次凭卡另收10元．
暑假普通票正常出售，两种优惠卡仅限暑假使用，不限次数．设游泳x次时，所需总费用为y元
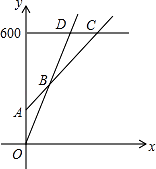(1)、分别写出选择银卡、普通票消费时，y与x之间的函数关系式；
(2)、在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点A、B、C的坐标；
(3)、请根据函数图象，直接写出选择哪种消费方式更合算．22. 综合题(1)、【问题发现】
如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE，
填空：①∠AEB的度数为 ；②线段AD、BE之间的数量关系是 ．
(2)、【拓展探究】如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°， 点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由．
(3)、【解决问题】
如图3，在正方形ABCD中，CD= ．若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．
23. 如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）.抛物线y=ax2+bx过A、C两点.
(1)、直接写出点A的坐标，并求出抛物线的解析式；(2)、动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P作PE⊥AB交AC于点E①过点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线段EG最长?
②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值.