河南省新乡市2018届数学中考一模试卷
试卷更新日期:2018-07-03 类型:中考模拟
一、单选题
-
1. ﹣3相反数是( )A、 B、﹣3 C、﹣ D、32. 下列四个图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 由6个小正方体搭成的几何体如图①所示,它的主视图是图②,则它的俯视图为( )
3. 由6个小正方体搭成的几何体如图①所示,它的主视图是图②,则它的俯视图为( ) A、
A、 B、
B、 C、
C、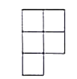 D、
D、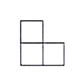 4. 移动支付被称为中国新四大发明之一,据统计我国目前每分钟移动支付金额达3.79亿元,将数据3.79亿用科学记数法表示为( )A、3.79×108 B、37.9×107 C、3.79×106 D、379×1065. 如图,AB∥CD,点E在AB上,点F在CD上,EF⊥FH,FH与AB相交于点G,若∠CFE=40°,则∠EGF的( )
4. 移动支付被称为中国新四大发明之一,据统计我国目前每分钟移动支付金额达3.79亿元,将数据3.79亿用科学记数法表示为( )A、3.79×108 B、37.9×107 C、3.79×106 D、379×1065. 如图,AB∥CD,点E在AB上,点F在CD上,EF⊥FH,FH与AB相交于点G,若∠CFE=40°,则∠EGF的( )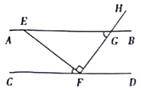 A、40° B、50° C、60° D、70°6. 下列计算正确的是( )A、a2•a3=a6 B、(a2)4=a6 C、(2a2b)3=8a6b3 D、4a3b6÷2ab2=2a2b37. 在一次中学生汉字听写大赛中,某中学代表队6名同学的笔试成绩分别为:75,85,91,85,95,85.关于这6名学生成绩,下列说法正确的是( )A、平均数是87 B、中位数是88 C、众数是85 D、方差是2308. 抛物线y=(x﹣1)2+3的顶点坐标是( )
A、40° B、50° C、60° D、70°6. 下列计算正确的是( )A、a2•a3=a6 B、(a2)4=a6 C、(2a2b)3=8a6b3 D、4a3b6÷2ab2=2a2b37. 在一次中学生汉字听写大赛中,某中学代表队6名同学的笔试成绩分别为:75,85,91,85,95,85.关于这6名学生成绩,下列说法正确的是( )A、平均数是87 B、中位数是88 C、众数是85 D、方差是2308. 抛物线y=(x﹣1)2+3的顶点坐标是( )
A、(1,3) B、(﹣1,3) C、(﹣1,﹣3) D、(1,﹣3)9. 有4张全新的扑克牌,其中黑桃、红桃各2张,它们的背面都一样,将它们洗匀后,背面朝上放到桌面上,从中任意摸出2张牌,摸出的花色不一样的概率是( )
A、 B、 C、 D、10. 如图,平行四边形ABCD中,AB= cm,BC=2cm,∠ABC=45°,点P从点B出发,以1cm/s的速度沿折线BC→CD→DA运动,到达点A为止,设运动时间为t(s),△ABP的面积为S(cm2),则S与t的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 计算: ﹣|2﹣ |=12. 一次函数y=(k−2)x+3−k的图象经过第一、二、三象限,则k的取值范围是。
13. 如图,▱ABCD中,点E、F分别在BC,AD上,且BE:EC=2:1,EF∥CD,交对角线AC于点G,则 = . 14. 如图所示,半圆O的直径AB=4,以点B为圆心, 为半径作弧,交半圆O于点C,交直径AB于点D,则图中阴影部分的面积是.
14. 如图所示,半圆O的直径AB=4,以点B为圆心, 为半径作弧,交半圆O于点C,交直径AB于点D,则图中阴影部分的面积是. 15. 菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为。
15. 菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为。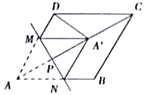
三、解答题
-
16. 先化简,再求值:( )÷ ,其中a= +1,b= ﹣1.17. 2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
调查结果统计表
组别
成绩分组(单位:分)
频数
频率
A
80≤x<85
50
0.1
B
85≤x<90
75
C
90≤x<95
150
c
D
95≤x≤100
a
合计
b
1
根据以上信息解答下列问题:
 (1)、统计表中,a= , b= , c=;(2)、扇形统计图中,m的值为 , “C”所对应的圆心角的度数是;
(1)、统计表中,a= , b= , c=;(2)、扇形统计图中,m的值为 , “C”所对应的圆心角的度数是;
(3)、若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?
18. 如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E使AE∥BC,连接AE。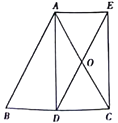 (1)、求证:四边形ADCE是矩形;(2)、①若AB=17,BC=16,则四边形ADCE的面积=;
(1)、求证:四边形ADCE是矩形;(2)、①若AB=17,BC=16,则四边形ADCE的面积=;②若AB=10,则BC=时,四边形ADCE是正方形。
19. 如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都在坐标轴上,点B的坐标是(4.2),反比例函数 与AB,BC分别交于点D,E。 (1)、求直线DE的解析式;(2)、若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。20. 如图,为探测某座山的高度AB,某飞机在空中C处测得山顶A处的俯角为31°,此时飞机的飞行高度为CH=4千米;保持飞行高度与方向不变,继续向前飞行2千米到达D处,测得山顶A处的俯角为50°,求此山的高度AB.(参考数据:tan31°≈0.6,tan50°≈1.2)
(1)、求直线DE的解析式;(2)、若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。20. 如图,为探测某座山的高度AB,某飞机在空中C处测得山顶A处的俯角为31°,此时飞机的飞行高度为CH=4千米;保持飞行高度与方向不变,继续向前飞行2千米到达D处,测得山顶A处的俯角为50°,求此山的高度AB.(参考数据:tan31°≈0.6,tan50°≈1.2) 21. 某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
21. 某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)、篮球和排球的单价各是多少元?(2)、若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
22. 如图①,在△ABC与△ADE中,AB=AC,AD=AE,∠A是公共角。 (1)、BD与CE的数量关系是:BDCE;(2)、把图①△ABC绕点A旋转一定的角度,得到如图②所示的图形。
(1)、BD与CE的数量关系是:BDCE;(2)、把图①△ABC绕点A旋转一定的角度,得到如图②所示的图形。①求证:BD=CE;
②BD与CE所在直线的夹角与∠DAE的数量关系是什么?说明理由。(3)、若AD=10,AB=6,把图①中的△ABC绕点A顺时针旋转α度(0°<α≤360)直接写出BD长度的取值范围。
23. 如图,一次函数 分别交y轴、x 轴于A、B两点,抛物线 过A、B两点.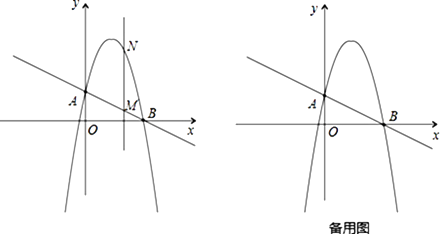 (1)、求这个抛物线的解析式;(2)、作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?(3)、在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
(1)、求这个抛物线的解析式;(2)、作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?(3)、在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.