山东省泰安市2018年中考数学试卷
试卷更新日期:2018-07-03 类型:中考真卷
一、选择题
-
1. 计算: 的结果是( )
A、-3 B、0 C、-1 D、32. 下列运算正确的是( )A、 B、 C、 D、3. 如图是下列哪个几何体的主视图与俯视图( )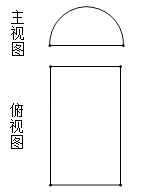 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,将一张含有 角的三角形纸片的两个顶点叠放在矩形的两条对边上,若 ,则 的大小为( )
4. 如图,将一张含有 角的三角形纸片的两个顶点叠放在矩形的两条对边上,若 ,则 的大小为( )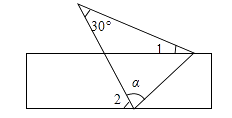 A、 B、 C、 D、5. 某中学九年级二班六级的8名同学在一次排球垫球测试中的成绩如下(单位:个)
A、 B、 C、 D、5. 某中学九年级二班六级的8名同学在一次排球垫球测试中的成绩如下(单位:个)35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A、42、42 B、43、42 C、43、43 D、44、436. 夏季来临,某超市试销 , 两种型号的风扇,两周内共销售30台,销售收入5300元, 型风扇每台200元, 型风扇每台150元,问 , 两种型号的风扇分别销售了多少台?若设 型风扇销售了 台, 型风扇销售了 台,则根据题意列出方程组为( )
A、 B、 C、 D、7. 二次函数 的图象如图所示,则反比例函数 与一次函数 在同一坐标系内的大致图象是( ) A、
A、 B、
B、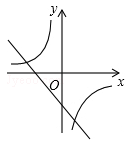 C、
C、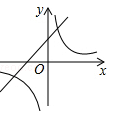 D、
D、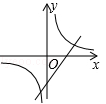 8. 不等式组 有3个整数解,则 的取值范围是( )
8. 不等式组 有3个整数解,则 的取值范围是( )
A、 B、 C、 D、9. 如图, 与 相切于点 ,若 ,则 的度数为( ) A、 B、 C、 D、10. 一元二次方程 根的情况是( )
A、 B、 C、 D、10. 一元二次方程 根的情况是( )
A、无实数根 B、有一个正根,一个负根 C、有两个正根,且都小于3 D、有两个正根,且有一根大于311. 如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1, 经过平移后得到 ,若 上一点 平移后对应点为 ,点 绕原点顺时针旋转 ,对应点为 ,则点 的坐标为( )
A、 B、 C、 D、12. 如图, 的半径为2,圆心 的坐标为 ,点 是 上的任意一点, ,且 , 与 轴分别交于 , 两点,若点 ,点 关于原点 对称,则 的最小值为( )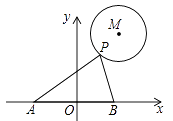
A、3 B、4 C、6 D、8二、填空题
-
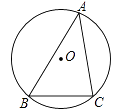
13. 一个铁原子的质量是 ,将这个数据用科学记数法表示为 .14. 如图, 是 的外接圆, , ,则 的直径为 .
 15. 如图,在矩形 中, , ,将矩形 沿 折叠,点 落在 处,若 的延长线恰好过点 ,则 的值为 .
15. 如图,在矩形 中, , ,将矩形 沿 折叠,点 落在 处,若 的延长线恰好过点 ,则 的值为 .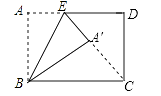 16. 观察“田”字中各数的关系:
16. 观察“田”字中各数的关系:
则C的值为 。
17. 如图,在 中, , , ,点 是 边上的动点(不与点 重合),过 作 ,垂足为 ,点 是 的中点,连接 ,设 , 的面积为 ,则 与 之间的函数关系式为 . 18. 《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
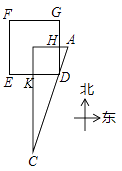
18. 《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图, 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门 位于 的中点,南门 位于 的中点,出东门15步的 处有一树木,求出南门多少步恰好看到位于 处的树木(即点 在直线 上)?请你计算 的长为步.
三、解答题
-
19. 先化简,再求值: ,其中 .20. 文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)、甲乙两种图书的售价分别为每本多少元?(2)、书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
21. 为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取了一个班学生的成绩进行整理,分为 , , , 四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)、请估计本校初三年级等级为 的学生人数;(2)、学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.22. 如图,矩形 的两边 、 的长分别为3、8, 是 的中点,反比例函数 的图象经过点 ,与 交于点 .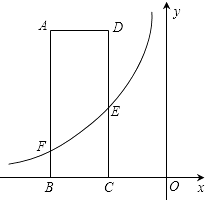 (1)、若点 坐标为 ,求 的值及图象经过 、 两点的一次函数的表达式;(2)、若 ,求反比例函数的表达式.23. 如图, 中, 是 上一点, 于点 , 是 的中点, 于点 ,与 交于点 ,若 , 平分 ,连接 , .
(1)、若点 坐标为 ,求 的值及图象经过 、 两点的一次函数的表达式;(2)、若 ,求反比例函数的表达式.23. 如图, 中, 是 上一点, 于点 , 是 的中点, 于点 ,与 交于点 ,若 , 平分 ,连接 , . (1)、求证: ;(2)、小亮同学经过探究发现: .请你帮助小亮同学证明这一结论.(3)、若 ,判定四边形 是否为菱形,并说明理由.24. 如图,在平面直角坐标系中,二次函数 交 轴于点 、 ,交 轴于点 ,在 轴上有一点 ,连接 .
(1)、求证: ;(2)、小亮同学经过探究发现: .请你帮助小亮同学证明这一结论.(3)、若 ,判定四边形 是否为菱形,并说明理由.24. 如图,在平面直角坐标系中,二次函数 交 轴于点 、 ,交 轴于点 ,在 轴上有一点 ,连接 . (1)、求二次函数的表达式;(2)、若点 为抛物线在 轴负半轴上方的一个动点,求 面积的最大值;
(1)、求二次函数的表达式;(2)、若点 为抛物线在 轴负半轴上方的一个动点,求 面积的最大值;
(3)、抛物线对称轴上是否存在点 ,使 为等腰三角形,若存在,请直接写出所有 点的坐标,若不存在请说明理由.
25. 如图,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF//AB,∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G.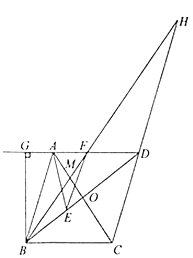 (1)、∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;(2)、找出图中与ΔAGB相似的三角形,并证明;(3)、BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MF⋅MH.
(1)、∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;(2)、找出图中与ΔAGB相似的三角形,并证明;(3)、BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MF⋅MH.