贵州省黔西南州兴义市2017-2018学年八年级下学期数学期中考试试卷

试卷更新日期：2018-07-03 类型：期中考试

进入出卷网下载

一、选择题．

1. 下列式子为最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{2}$ C、 $\sqrt{2^{2}}$ D、 $\sqrt{4}$

查看试题解析
2. 以下各式不是代数式的是（）

A、0 B、 $\frac{x}{y}$ C、 $\frac{1}{2} > \frac{1}{3}$ D、 $\sqrt{11}$

查看试题解析
3. 在 $△$ ABC，如果AC²-AB²=BC² ，那么（）

A、 $∠$ A= $90^{\circ}$ B、 $∠$ B= $90^{\circ}$ C、 $∠$ C= $90^{\circ}$ D、不能确定

查看试题解析
4. 如果 $\sqrt{18 x}$ 是一个整数，那么x可取的最小正整数的值（）

A、2 B、3 C、4 D、8

查看试题解析
5. 如图，以Rt $△$ ABC的三边为边向外作正方形，其面积分别为S₁、S₂、S₃ ，且S₁=64，S₃=289，则s₂为（）

A、15 B、25 C、81 D、225

查看试题解析
6. 估计 $\sqrt{32} \times \sqrt{\frac{1}{2}} + \sqrt{20}$ 的运算结果是（）

A、6与7之间 B、7与8之间 C、8与9之间 D、9与10之间

查看试题解析
7.
如图，在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段，其中能构成一个直角三角形三边的线段是（　　）

A、CD、EF、GH B、AB、EF、GH C、AB、CD、GH D、AB、CD、EF

查看试题解析
8. 计算 ${(\sqrt{3} + 2)}^{2017} {(\sqrt{3} - 2)}^{2018}$ 的结果是（）

A、 $2 + \sqrt{3}$ B、 $\sqrt{3} - 2$ C、 $2 - \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
9. 实数a在数轴上的位置如图所示，则 $\sqrt{{(a - 4)}^{2}} + \sqrt{{(a - 11)}^{2}}$ 的化简结果为（）

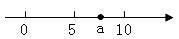A、7 B、-7 C、2a-15 D、无法化简

查看试题解析
10. 如图，长方形纸片ABCD中，AD=4cm，把纸片沿直线AC折叠，点B落在E处，AE交DC于点O，若AO=5cm，则AB的长为（）

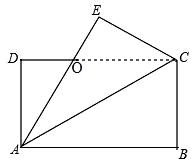A、6cm B、7cm C、8cm D、9cm

查看试题解析

二、填空题。

11. 写出命题“若a=b，则a²=b²”的逆命题

查看试题解析
12. 计算 $\sqrt{{(- 5)}^{2}}$ 的结果是

查看试题解析
13. 若长方形相邻两边的长分别是 $\sqrt{20}$ cm和 $\sqrt{125}$ cm，则它的周长是 cm．

查看试题解析
14. 下列各组数：①1、2、3；②6、8、10；③0.3、0.4、0.5；④9、40、41；其中是勾股数的有 (填序号)

查看试题解析
15. 学校有一块长方形花圃，有极少数人为了避免拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了步路(假设2步为1米)，却踩伤了花草．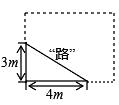

查看试题解析
16. 若 $\sqrt{\frac{x - 2}{3 - x}} = \frac{\sqrt{x - 2}}{\sqrt{3 - x}}$ 成立，则x满足

查看试题解析
17. 若 $a - \frac{1}{a} = \sqrt{2017}$ ，则 $a + \frac{1}{a} =$

查看试题解析
18. 有一个边长为2m的正方形洞口，想用一个圆形盖去盖住这个洞口，圆形盖的半径至少是 m．

查看试题解析
19. 对于任意不相等的两个实数a、b，定义运算※如下：a※b= $\frac{\sqrt{a + b}}{a - b}$ ，例如3※2= $\frac{\sqrt{3 + 2}}{3 - 2}$ 那么8※12=

查看试题解析
20. 如图，0P=1，过点P作PP ₁ $⊥$ OP且PP₁=1得OP₁= $\sqrt{2}$ ；再过P₁ ，作P₁P₂ $⊥$ OP₁且P₁P₂=1，得OP₂= $\sqrt{3}$ ；又过P₂作P₂P₃ $⊥$ OP₂且P₂P₃=1，得0P₃=2；……依此法继续作下去，得OP₂₀₁₃=

查看试题解析

三、解答题．

21.

(1)、 $5 \sqrt{\frac{1}{5}} + 2 \sqrt{20} - \sqrt{\frac{5}{2}}$

(2)、 $\sqrt{\frac{7}{11}} \times (\sqrt{\frac{11}{7}} \div \sqrt{\frac{1}{11}})$

查看试题解析
22. 在Rt $△$ ABC中， $∠$ C= $90^{\circ}$ ，a、b、C分别是 $∠$ A、 $∠$ B、 $∠$ C所对的三条边．

(1)、已知a= $\sqrt{7}$ ，b=3，求C的长；

(2)、已知c=13，b=12，求a的长．

查看试题解析
23. 先化简，再求值： $(a^{2} b + a b) \div \frac{a^{2} + 2 a + 1}{a + 1}$ ，其中 $a = \sqrt{3} + 1 ， b = \sqrt{3} - 1$

查看试题解析
24. 如图，某工厂C前面有一条笔直的公路，原来有两条路AC、BC可以从工厂C到达公路，经测量AC=600m，BC=800m，AB=1000m，现需要修建一条路，使工厂C到公路的距离最短，请你帮工厂C的负责人设计一种方案，并求出新建的路的长．

查看试题解析
25. 如图，在△ABD中， $∠$ D=90^° ， C是BD上一点，已知BC=9，AB=17，AC=10，求AD的长。

查看试题解析
26. 阅读下面的问题：
$\begin{array}{l} \frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1 ； \\ \frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2} ； \\ \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3} ； \\ \dots \dots \end{array}$

(1)、求 $\frac{1}{\sqrt{7} + \sqrt{6}}$ 与 $\frac{1}{\sqrt{7} - \sqrt{6}}$ 的值；

(2)、已知n是正整数，求 $\frac{1}{\sqrt{n+1} + \sqrt{n}}$ 与 $\frac{1}{\sqrt{n+1} - \sqrt{n}}$ 的值；

(3)、计算 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \dots \dots + \frac{1}{\sqrt{99} + \sqrt{98}} + \frac{1}{\sqrt{100} + \sqrt{99}}$

查看试题解析