浙江省临海市2016学年上学期九年级期末调研测试数学
试卷更新日期：2017-01-19 类型：期末考试
一、选择题
-
1.
为了迎接在崇和门广场举行的“中国·临海无核蜜桔节”开幕式，某校学生设计了如图所示的宣传图标，图标中的字母是中心对称图形的是（ ）
A、L B、H C、Y D、Q2. 下列方程中，关于x的一元二次方程的是（ ）
A、x-2=0 B、x+y=3 C、x2+xy=0 D、x2=9-2x3. 气象台预报“本市明天降水概率是90%”，对此消息下列说法正确的是（ ）
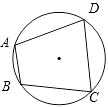
A、本市明天降水可能性很大 B、本市明天将有90%的时间降水 C、本市明天肯定降水 D、本市明天将有90%的地区降水4.如图，四边形ABCD是圆内接四边形，若∠BAD ＝105°，则∠BCD的度数是（ ）
A、105° B、95° C、75° D、60°5. 若二次函数y=-2x2+bx+c的顶点坐标为（2，-3），则此函数有（ ）
A、最大值2 B、最大值-3 C、最小值2 D、最小值-36. 从正方形的四个顶点中，任取三个顶点连成三角形．把“这个三角形是等边三角形”记作事件M，下列判断正确的是（ ）
A、事件M是不可能事件 B、事件M是必然事件 C、事件M发生的概率为 D、事件M发生的概概率为7. 关于x的一元二次方程x2+a=0没有实数根，则实数a的取值范围是（ ）
A、a≤0 B、a≥0 C、a＜0 D、a＞08.如图，△OAB绕点O逆时针旋转80°得到△OCD，若∠A=40°，∠D=110°，则∠α的度数是（ ）
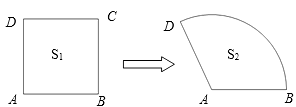
A、30° B、40° C、50° D、60°9.如图，四边形ABCD是由铁丝围成的正方形，现将边BC，CD变成圆弧BD，成为一个扇形ABD，记正方形的面积为S1 ， 扇形的面积为S2 ， 则S1与S2的大小关系为（ ）
A、S1>S2 B、S1=S2 C、S1<S2 D、无法确定10. 一个不透明的袋子中有5个完全相同的小球，球上分别标着点A（-2，0），B（1，0），C（4，0），D（0，-6），E（-2，3）．从袋子中一次性随机摸出3个球，这3个球分别代表的点恰好能确定一条抛物线（对称轴平行于y轴）的概率是（ ）
A、 B、 C、 D、二、填空题
-
11. 点P（2，-5）关于原点的对称点Q的坐标为 ．
12. 已知⊙O的半径为5厘米，当OP=6厘米时，点P在⊙O ． （填“内”或“外”或“上”）
13. 下表记录了篮球运动员易建联在某段时间内进行定点投篮训练的结果：投篮次数
10
100
10000
投中次数
9
89
9012
试估计易建联定点投篮一次，投中的概率约是 ． （精确到0.1）
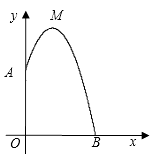
14.某幢建筑物，从10米高的窗口A用水管向外喷水，喷出的水流呈抛物线状（抛物线所在平面与墙面垂直，如图所示），如果抛物线的最高点M离墙1米，离地面12米，则水流落地点B离墙的距离OB是米．
15. 当x=m或x=n（m≠n）时，代数式x2-2x的值相等，则当x=m+n时，代数式x2-2x的值为 ．
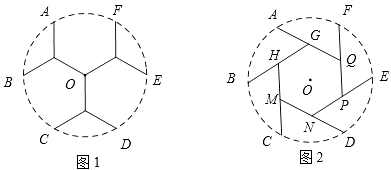
16.已知A，B，C，D，E，F分别是⊙O上的六等分点，⊙O的半径是100，在这六点间修建互通的道路（即图中实线部分为道路），现有如下两种方案．方案一：如图1，各条线段长度均相等，记图中道路长为l1；方案二：如图2，AQ=BG=CH=DM=EN=FP，点G，H，M，N，P，Q分别是线段AQ，BG，CH，DM，EN，FP的中点，六边形GHMNPQ是以O为中心的正六边形，记图中道路长为l2；则l1= ；l2= ．
三、解答题吧
-
17. 解方程：(1)、x2+2x=0；(2)、x2-x-1=0．18. 已知抛物线y=x2+bx+4经过点（2，-2）．
(1)、求出这个抛物线的解析式；
(2)、求这个抛物线的顶点坐标．19. 九年级某班同学小明和小林将被保送到台州中学的A、B班级，他们希望能再次成为同班同学．(1)、请你用画树状图法或列表法，列出所有可能的结果；
(2)、求他们再次成为同班同学的概率．
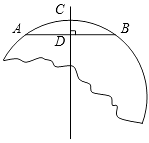
20.如图，在破残的圆形残片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D，已知AB=8 cm，CD=2 cm．求破残的圆形残片的半径．
21. 每年淘宝网都会举办“双十一”购物狂欢节，许多商家都会利用这个契机进行打折让利的促销活动．甲网店销售一件A商品的成本为36元，网上标价为110元．“双十一”活动当天，为了吸引买主，连续两次降价销售A商品，问平均每次降价率为多少时，才能使这件A商品的利润率为10%？22. 已知△ABC是等边三角形．(1)、动手操作：如图1，点D在△ABC内，且∠BDC=150°，CD=1，BD= ， 把△BCD绕着点C顺时针旋转，使点B旋转到点A，得到△AEC．
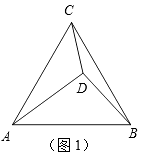
①依题意补全图1；（确认无误后，请用黑色水笔描黑）
②连接DE，则线段DE= ， AD=；
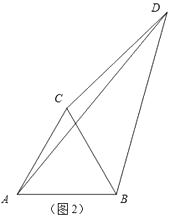
(2)、应用拓展：如图2，点D在△ABC外，且CD=3，BD=4，AD=5，求∠BDC的度数．
23.如图，矩形ABCD的边AB=4，且BC＞AB，一个量角器如图所示放置，其中零刻度（即半圆O的直径）与边AB重合，点A处是0刻度，点B处是180刻度，点P是量角器的半圆弧上一动点，过点P作半圆的切线，设点P的刻度数为m，过点P的切线交线段BC与线段AD于点E，F．
(1)、设∠PAB=n．①如图1，当m=114°时，n=；
②直接写出n与m的关系式：；
(2)、试说明AF·BE是否是一个定值，若是，请求出它的值；若不是，请说明理由；(3)、当EF= 时，求点P的刻度数m的值．24.定义：两条抛物线顶点都在直线y=x上，且两条抛物线关于原点成中心对称，则称这两条抛物线为一对“友好抛物线”．
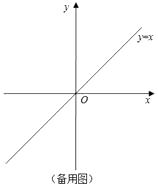(1)、抛物线y=2（x-1）2+1如图1所示，请画出它的“友好抛物线”，并直接写出它的解析式；（确认无误后，请用黑色水笔描黑）
(2)、一对“友好抛物线”，其中一条抛物线的解析式为y= -（x+h）2-h，这对“友好抛物线”与y轴交点记为A，B，记AB=n（当A与B重合时，记n=0），现我们来探究n与h的关系；①当h≥0时，如图2所示，求n与h的函数关系式；
②当h＜0时，求n与h的函数关系式；
(3)、在（2）的条件下，要使 ≤n≤ ，试直接写出h的取值范围．