2016年湖南省张家界市中考数学模拟试卷（二）
试卷更新日期：2017-01-19 类型：中考模拟
一、选择题
-
1. 一个数的相反数是﹣2016，则这个数是（ ）A、2016 B、﹣2016 C、 D、2. 若点P（x0 ， y0）在函数y= （x＜0）的图象上，且x0y0=﹣1．则它的图象大致是（ ）A、
B、
C、
D、
3. 如图，已知∠1=50°，如果CD∥BE，那么∠B的度数是（ ）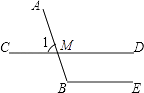
A、50° B、100° C、120° D、130°4. 某次捐款活动中，7位同学的捐款金额分别是5元，6元，6元，7元，8元，9元，10元，则这组数据的中位数与众数分别是（ ）A、6，6 B、7，6 C、7，8 D、6，85. 在▱ABCD中，点E为AD的中点，连接BE，交AC于点F，则AF：CF=（ ）
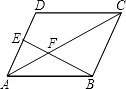A、1：2 B、1：3 C、2：3 D、2：56. 如图几何体中，主视图、左视图、俯视图为同一种图形的是（ ）A、
B、
C、
D、
7. 若关于x的方程 =1无解，则a的值为（ ）A、0 B、1 C、2 D、48. 如图，△ABC中，∠ACB=90°，AC=BC=1，取斜边的中点，向斜边作垂线，画出一个新的等腰Rt△，如此继续下去，直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止，此时，这个直角三角形的斜边长为（ ）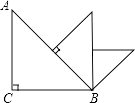
A、 B、 C、 D、二、填空题
-
9. 地球上的海洋面积约为36105.9万平方千米，用科学记数法（保留三个有效数字）表示为 平方千米．10. 因式分解：a3﹣a= ．11. 甲，乙两支球队的人数相等，平均身高都是1.72米，方差分别是S甲2=0.35，S乙2=0.27，则甲、乙两队中身高较整齐的是队．12. 如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=3，则菱形ABCD的周长是 ．
13. 如图，如果曲线l1是反比例函数y= 在第一象限内的图象，且过点A（2，1），那么l1关于x轴对称的曲线l2的解析式为 ．
14. 若关于x的方程x2﹣2 x﹣k=0有两个相等的实数根，则k的值为 ．15. 如图，半圆O的直径在梯形ABCD的底边AB上，并且与其余三边AD，CD，BC都相切．若BC=2，DA=3，则AB=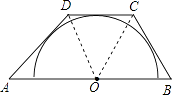
16. 如图，⊙O的直径为10cm，弦AB为6cm，点P为弦上的一动点，若OP的长为整数，则OP的可能值是
三、解答下列各题
-
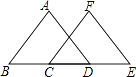
17. 计算： +（ ）﹣1﹣2cos60°+（3﹣π）0 ．18. 先化简，再求值 ，其中x= ．19. 如图，点B，C，D，E在同一直线上，并且BC=DE．若AB=CF，AD=EF．试探索AB与FC的位置关系，并说明理由．
20. 某市需铺设长为1000米的地下管道，决定由甲、乙两个工程队来完成这一工程．已知甲工程队比乙工程队每天多铺设20米，且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同．求甲工程队每天铺设多少米？21. 某数学小组用高为1.2米的仪器测量一教学楼的高CD，如图，距CD一定距离的A处，用仪器测得教学楼顶部D的仰角为β，再在A与C之间选一点B，由B处测出教学楼顶部D的仰角为α，测得A，B之间的距离为4米，若tanα=1.6，tanβ=1.2，则他们能求出教学楼的高吗？
22. 如图所示，方格纸中的每个小方格都是边长为1的正方形，Rt△ABC的顶点均在格点上．A（﹣6，1）B（﹣3，1）C（﹣3，3）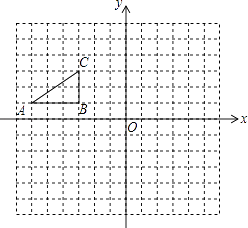
(1)、将Rt△ABC沿x轴正方向平移5个单位长度后得到Rt△A1B1C1 ． 试在图中画出Rt△A1B1C1 ， 并写出C1点的坐标；(2)、将Rt△ABC绕点B顺时针旋转90°后得到Rt△A2B2C2 ． 试在图中画出Rt△A2B2C2 ．23. 某记者在某区随机选取了几个停车场对开车司机进行了相关的调查，本次调查结果有四种情形：A．喝酒后开车 B．喝酒后不开车或请代驾 C．开车当天不喝酒 D．从不喝酒
将这次调查情况整理并绘制了如下尚不完整的两个统计图．请根据相关信息，解答下列问题：
(1)、该记者本次一共调查了名司机；(2)、图1中情况D所在扇形的圆心角为°；
(3)、补全图2；
(4)、本次调查中，记者随机采访其中的一名司机，则他属于情况C的概率是(5)、若该区有3万名司机，则其中不违反“酒驾”禁令的人数约为人．24.如图，已知二次函数y=x2+bx+c的图象与x轴交于A，B两点，与y轴交于点P，顶点为C（1，﹣2）．
(1)、求此函数的关系式；(2)、作点C关于x轴的对称点D，顺次连接A，C，B，D．若在抛物线上存在点E，使直线PE将四边形ACBD分成面积相等的两个四边形，求点E的坐标；(3)、在（2）的条件下，抛物线上是否存在一点F，使得△PEF是以P为直角顶点的直角三角形？若存在，求出点F的坐标及△PEF的面积；若不存在，请说明理由．