2016年山东省潍坊市高考数学三模试卷（理科）

试卷更新日期：2017-01-18 类型：高考模拟

进入出卷网下载

一、选择题：

1. 已知全集U=R，A={x|x²﹣5x+6≥0}，则∁_UA=（）

A、{x|x＞2} B、{x|x＞3或x＜2} C、{x|2≤x≤3} D、{x|2＜x＜3}

查看试题解析
2. 设复数z满足（2﹣i）z=5i（i为虚数单位），则复数z在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知a，b∈R，则“0≤a≤1且0≤b≤1”是“0≤ab≤1”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 已知向量 $\vec{a}$ ， $\vec{b}$ 的夹角为60°，且| $\vec{a}$ |=1，|2 $\vec{a}$ ﹣ $\vec{b}$ |= $\sqrt{3}$ ，则| $\vec{b}$ |=（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
5. 在一次数学竞赛中，30名参赛学生的成绩（百分制）的茎叶图如图所示：若将参赛学生按成绩由高到低编为1﹣30号，再用系统抽样法从中抽取6人，则其中抽取的成绩在[77，90]内的学生人数为（）

A、2 B、3 C、4 D、5

查看试题解析
6. 如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法，执行该程序框图，则输出的结果S表示的值为（）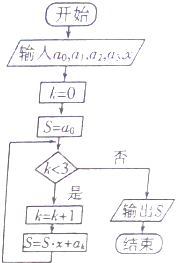

A、a₀+a₁+a₂+a₃ B、（a₀+a₁+a₂+a₃）x³ C、a₀+a₁x+a₂x²+a₃x³ D、a₀x³+a₁x²+a₂x+a₃

查看试题解析
7. 已知函数f（x）=sin2ωx（ω＞0），将y=f（x）的图象向右平移 $\frac{π}{4}$ 个单位长度后，若所得图象与原图象重合，则ω的最小值等于（）

A、2 B、4 C、6 D、8

查看试题解析
8. 给出以下四个函数的大致图象：则函数f（x）=xlnx，g（x）= $\frac{\ln x}{x}$ ，h（x）=xe^x ， t（x）= $\frac{e^{x}}{x}$ 对应的图象序号顺序正确的是（）

A、②④③① B、④②③① C、③①②④ D、④①②③

查看试题解析
9. 在一次抽奖活动中，8张奖券中有一、二、三等奖各1张，其余5张无奖．甲、乙、丙、丁四名顾客每人从中抽取2张，则不同的获奖情况有（）

A、24种 B、36种 C、60种 D、96种

查看试题解析
10. 已知F₁ ， F₂为椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右焦点，以原点O为圆心，半焦距为半径的圆与椭圆相交于四个点，设位于y轴右侧的两个交点为A，B，若△ABF₁为等边三角形，则椭圆的离心率为（）

A、 $\sqrt{2}$ ﹣1 B、 $\sqrt{3}$ ﹣1 C、 $\frac{\sqrt{2} - 1}{2}$ D、 $\frac{\sqrt{3} - 1}{3}$

查看试题解析

二、填空题：

11. 若存在实数x使|x﹣a|+|x|≤4成立，则实数a的取值范围是．

查看试题解析
12. 已知函数f（x）= $\frac{e^{x} - m}{e^{x} + 1}$ +mx是定义在R上的奇函数，则实数m= ．

查看试题解析
13. 圆心在x轴的正半轴上，半径为双曲线 $\frac{x^{2}}{16} - \frac{y^{2}}{9}$ =1的虚半轴长，且与该双曲线的渐近线相切的圆的方程是．

查看试题解析
14. 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积为．

查看试题解析
15. 已知函数h（x）=x²+ax+b在（0，1）上有两个不同的零点，记min{m，n}= ${\begin{matrix} m (m \leq n) \\ n (m > n) \end{matrix}$ ，则min{h（0），h（1）}的取值范围为．

查看试题解析

三、解答题：

16. 在△ABC中，内角A，B，C的对边分别为a，b，c，且3cosAcosB+1=3sinAsinB+cos2C．

(1)、求∠C

(2)、若△ABC的面积为5 $\sqrt{3}$ ，b=5，求sinA．

查看试题解析
17. 如图，已知四棱锥P﹣ABCD中，底面ABCD是直角梯形，∠ADC=90°，AB∥CD，AD=DC= $\frac{1}{2}$ AB= $\sqrt{2}$ ，平面PBC⊥平面ABCD．

(1)、求证：AC⊥PB；

(2)、若PB=PC= $\sqrt{2}$ ，问在侧棱PB上是否存在一点M，使得二面角M﹣AD﹣B的余弦值为 $\frac{5 \sqrt{3}}{9}$ ？若存在，求出 $\frac{P M}{P B}$ 的值；若不存在，说明理由．

查看试题解析
18. 某校在高二年级实行选课走班教学，学校为学生提供了多种课程，其中数学科提供5种不同层次的课程，分别称为数学1、数学2、数学3、数学4、数学5，每个学生只能从这5种数学课程中选择一种学习，该校高二年级1800名学生的数学选课人数统计如表：
课程
数学1
数学2
数学3
数学4
数学5
合计
选课人数
180
540
540
360
180
1800
为了了解数学成绩与学生选课情况之间的关系，用分层抽样的方法从这1800名学生中抽取了10人进行分析．

(1)、从选出的10名学生中随机抽取3人，求这3人中至少有2人选择数学2的概率；

(2)、从选出的10名学生中随机抽取3人，记这3人中选择数学2的人数为X，选择数学1的人数为Y，设随机变量ξ=X﹣Y，求随机变量ξ的分布列和数学期望E（ξ）．

查看试题解析
19. 如表是一个由n²个正数组成的数表，用a_ij表示第i行第j个数（i，j∈N），已知数表中第一列各数从上到下依次构成等差数列，每一行各数从左到右依次构成等比数列，且公比都相等．已知a₁₁=1，a₃₁+a₆₁=9，a₃₅=48．

(1)、求a_n1和a_4n；

(2)、设b_n= $\frac{a_{4 n}}{(a_{4 n} - 2) (a_{4 n} - 1)}$ +（﹣1）ⁿ•a $_{n_{1}}$ （n∈N₊），求数列{b_n}的前n项和S_n ．

查看试题解析
20. 在平面直角坐标系中内动点P（x，y）到圆F：x²+（y﹣1）²=1的圆心F的距离比它到直线y=﹣2的距离小1．

(1)、求动点P的轨迹方程；

(2)、设点P的轨迹为曲线E，过点F的直线l的斜率为k，直线l交曲线E于A，B两点，交圆F于C，D两点（A，C两点相邻）．
①若 $\vec{B F}$ =t $\vec{F A}$ ，当t∈[1，2]时，求k的取值范围；
②过A，B两点分别作曲线E的切线l₁ ， l₂ ，两切线交于点N，求△ACN与△BDN面积之积的最小值．

查看试题解析
21. 已知函数f（x）=lnx﹣x+ $\frac{a}{x}$ +1（a∈R）．

(1)、讨论f（x）的单调性与极值点的个数；

(2)、当a=0时，关于x的方程f（x）=m（m∈R）有2个不同的实数根x₁ ， x₂ ，证明：x₁+x₂＞2．

查看试题解析

课程	数学1	数学2	数学3	数学4	数学5	合计
选课人数	180	540	540	360	180	1800