2016年山东省德州市高考数学一模试卷(理科)
试卷更新日期:2017-01-18 类型:高考模拟
一、选择题
-
1. 已知复数z满足z•i=1+i(i是虚数单位),则复数z的共轭复数在复平面内所对应的点的坐标为( )A、(1,1) B、(﹣1,﹣1) C、(1,﹣1) D、(﹣1,1)2. 若全集U=R,集合A={x|x2﹣x﹣2≥0},B={x|log3(2﹣x)≤1},则A∩(∁UB)=( )A、{x|x<2} B、{x|x<﹣1或x≥2} C、{x|x≥2} D、{x|x≤﹣1或x>2}3. 已知p:“直线l的倾斜角 ”;q:“直线l的斜率k>1”,则p是q的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 不等式|x+1|﹣|x﹣5|<4的解集为( )A、(﹣∞,4) B、(﹣∞,﹣4) C、(4,+∞) D、(﹣4,+∞)5. 为了增强环保意识,某校从男生中随机制取了60人,从女生中随机制取了50人参加环保知识测试,统计数据如下表所示:
优秀
非优秀
总计
男生
40
20
60
女生
20
30
50
总计
60
50
110
附:x2=
P(K2≥k)
0.500
0.100
0.050
0.010
0.001
k
0.455
2.706
3.841
6.635
10.828
则有( )的把握认为环保知识是否优秀与性别有关.
A、90% B、95% C、99% D、99.9%6. 函数y= 的图象大致为( )A、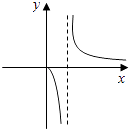 B、
B、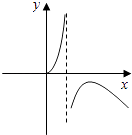 C、
C、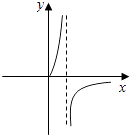 D、
D、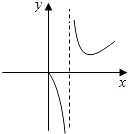 7. 已知双曲线与椭圆 的焦点重合,它们的离心率之和为 ,则双曲线的渐近线方程为( )A、 B、 C、 D、y=8. 已知点A(﹣2,0),B(2,0),若圆(x﹣3)2+y2=r2(r>0)上存在点P(不同于点A,B)使得PA⊥PB,则实数r的取值范围是( )A、(1,5) B、[1,5] C、(1,3] D、[3,5]9. 运行如图所示的程序框图,则输出的结果是( )
7. 已知双曲线与椭圆 的焦点重合,它们的离心率之和为 ,则双曲线的渐近线方程为( )A、 B、 C、 D、y=8. 已知点A(﹣2,0),B(2,0),若圆(x﹣3)2+y2=r2(r>0)上存在点P(不同于点A,B)使得PA⊥PB,则实数r的取值范围是( )A、(1,5) B、[1,5] C、(1,3] D、[3,5]9. 运行如图所示的程序框图,则输出的结果是( ) A、e2016﹣e2015 B、e2017﹣e2016 C、e2015﹣1 D、e2016﹣110. f(x)是定义在(0,+∞)上单调函数,且对∀x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是( )A、(0, ) B、( ,1) C、(1,e) D、(e,3)
A、e2016﹣e2015 B、e2017﹣e2016 C、e2015﹣1 D、e2016﹣110. f(x)是定义在(0,+∞)上单调函数,且对∀x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是( )A、(0, ) B、( ,1) C、(1,e) D、(e,3)二、填空题
-
11. 已知两个单位向量 的夹角为60°, , ,若 ,则正实数t= .12. 某三棱锥的三视图如图所示,其侧(左)视图为直角三角形,则该三棱锥外接球的表面积为 .
 13. 已知x,y满足 ,且z=2x﹣y的最大值是最小值的﹣2倍,则a的值是 .14. (x2+x+1)(1﹣x)4展开式中x2的系数为 .15. 若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)
13. 已知x,y满足 ,且z=2x﹣y的最大值是最小值的﹣2倍,则a的值是 .14. (x2+x+1)(1﹣x)4展开式中x2的系数为 .15. 若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)①y= ;②y= ;③y= ;④y= .
三、解答题
-
16. 已知函数f(x)=2 sin cos ﹣2sin2 (ω>0)的最小正周期为3π.
(I)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别为角A,B,C所对的边,a<b<c, a=2csinA,并且f( A+ )= ,求cosB的值.
17. 连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai , 若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.(1)、求你的幸运数字为3的概率;(2)、若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.18. 在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4 ,∠CDA=120°,点N在线段PB上,且PN=2. (1)、求证:BD⊥PC;(2)、求证:MN∥平面PDC;(3)、求二面角A﹣PC﹣B的余弦值.19. 已知数列{an}满足a1+2a2+3a3+…+nan=n(n∈N*).(1)、求数列{an}的通项公式an;(2)、令 ,写出Tn关于n的表达式,并求满足Tn> 时n的取值范围.20. 设函数 .(1)、用含a的式子表示b;(2)、令F(x)= ,其图象上任意一点P(x0 , y0)处切线的斜率 恒成立,求实数a的取值范围;(3)、若a=2,试求f(x)在区间 上的最大值.21. 已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆(x﹣5)2+y2=9的两条切线,切点为M,N,|MN|=3(1)、求抛物线E的方程;(2)、设A,B是抛物线E上分别位于x轴两侧的两个动点,且 (其中O为坐标原点).
(1)、求证:BD⊥PC;(2)、求证:MN∥平面PDC;(3)、求二面角A﹣PC﹣B的余弦值.19. 已知数列{an}满足a1+2a2+3a3+…+nan=n(n∈N*).(1)、求数列{an}的通项公式an;(2)、令 ,写出Tn关于n的表达式,并求满足Tn> 时n的取值范围.20. 设函数 .(1)、用含a的式子表示b;(2)、令F(x)= ,其图象上任意一点P(x0 , y0)处切线的斜率 恒成立,求实数a的取值范围;(3)、若a=2,试求f(x)在区间 上的最大值.21. 已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆(x﹣5)2+y2=9的两条切线,切点为M,N,|MN|=3(1)、求抛物线E的方程;(2)、设A,B是抛物线E上分别位于x轴两侧的两个动点,且 (其中O为坐标原点).①求证:直线AB必过定点,并求出该定点Q的坐标;
②过点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.