2016年福建省南平市建阳市中考数学模拟试卷

试卷更新日期：2017-01-18 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2016的绝对值是（）

A、﹣2016 B、2016 C、﹣ $\frac{1}{2016}$ D、 $\frac{1}{2016}$

查看试题解析
2. 如图所示的几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列图案中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 我区5月份连续五天的日最高气温（单位：℃）分别为：33，30，30，32，35．则这组数据的中位数和平均数分别是（）

A、32，32 B、32，33 C、30，31 D、30，32

查看试题解析
5. 某科研小组，为了考查某水库野生鱼的数量，从中捕捞100条，作上标记后，放回水库，经过一段时间，再从中捕捞300条，发现有标记的鱼有15条，则估计该水库中有野生鱼（）

A、8000条 B、4000条 C、2000条 D、1000条

查看试题解析
6. 下列多边形中，内角和是外角和的两倍的是（）

A、四边形 B、五边形 C、六边形 D、八边形

查看试题解析
7. 下列计算正确的是（）

A、a²•a³=a⁶ B、（﹣m²）³=﹣m⁶ C、b⁶÷b³=b² D、3a+3b=6ab

查看试题解析
8. 不等式组 ${\begin{matrix} x + 4 > 2 \\ 2 x - 5 < x \end{matrix}$ 的解集是（）

A、x＞﹣2 B、x＜5 C、x＜2 D、﹣2＜x＜5

查看试题解析
9. 直线y=﹣x+2沿y轴向上平移2个单位后与x轴的交点坐标是（）

A、（4，0） B、（0，4） C、（2，0） D、（0，2）

查看试题解析
10.
如图，在边长为1的正方形ABCD中，动点F，E分别以相同的速度从D，C两点同时出发向C和B运动（任何一个点到达即停止），过点P作PM∥CD交BC于M点，PN∥BC交CD于N点，连接MN，在运动过程中，则下列结论：
①△ABE≌△BCF；②AE=BF；③AE⊥BF；④CF²=PE•BF；⑤线段MN的最小值为 $\frac{\sqrt{5} - 1}{2}$ ．
其中正确的结论有（）

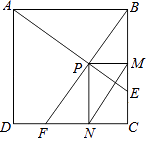A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 写出一个第二象限内的点的坐标：（，）．

查看试题解析
12. 想了解某电视台对正在播出的某电视节目收视率的情况，适合采用的调查方式是．（填“全面调查”或“抽样调查”）

查看试题解析
13. 计算： $\frac{x^{2}}{x - 1} = \frac{x}{x - 1}$ = ．

查看试题解析
14. 分解因式：3a²﹣6a+3= ．

查看试题解析
15. 已知圆锥的侧面积为15π，底面半径为3，则圆锥的高为．

查看试题解析
16. 如图，已知点A是双曲线y= $\frac{2}{x}$ 在第一象限的分支上的一个动点，连结AO并延长交另一分支于点B，以AB为斜边做等腰直角△ABC，点C在第四象限．随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y= $\frac{k}{x}$ （k＜0）上运动，则k的值是

查看试题解析

三、解答题

17. 计算： $\sqrt{4}$ ×（﹣2）²﹣2tan45°+（﹣2016）⁰ ．

查看试题解析
18. 先化简下列的代数式，再求值：[（2x+y）²+y（x﹣y）]÷x，其中x=1，y=1．

查看试题解析
19. 解分式方程： $\frac{2}{x}$ = $\frac{3}{2 x - 1}$ ．

查看试题解析
20. 如图，AB⊥BD于点B，ED⊥BD于点D，AE交BD于点C，且BC=DC．求证：AB=ED．

查看试题解析
21. 2016年为更好地宣传“开车不喝酒，喝酒不开车”的驾车理念，某市一家报社设计了如图的调查问卷（单选）．在随机调查了某市全部10000名司机中的部分司机后，统计整理并制作了如下的统计图：
根据以上信息解答下列问题：

(1)、补全条形统计图，并计算扇形统计图中m=；

(2)、该市支持选项C的司机大约有多少人？

(3)、若要从该市支持选项C的司机中随机选择200名，给他们签订“永不酒驾”的保证书，则支持该选项的司机小李被选中的概率是多少？

查看试题解析
22. 如图，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A，OE∥BD，交BC于点F，交AE于点E．

(1)、求证：△BEF∽△DBC．；

(2)、若⊙O的半径为3，∠C=32°，求BE的长．（精确到0.01）

查看试题解析
23. 2016年春季，建阳区某服装商店分两次从批发市场购进同一款服装，数量之比是2：3，且第一、二次进货价分别为每件50元、40元，总共付了4400元的货款．

(1)、求第一、二次购进服装的数量分别是多少件？

(2)、由于该款服装刚推出时，很受欢迎，按每件70元销售了x件；后来，由于该服装滞销，为了及时处理库存，缓解资金压力，其剩余部分的按每件30元全部售完．当x的值至少为多少时，该服装商店才不会亏本．

查看试题解析
24.
如图，抛物线y=﹣x²+bx+c与x轴交于点A（﹣1，0），B（5，0）两点，直线y=﹣ $\frac{3}{4}$ x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．

(1)、求抛物线的解析式；

(2)、若PE=5EF，求m的值；

(3)、若点E′是点E关于直线PC的对称点，是否存在点P，使点E′落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．

查看试题解析
25.
如图，在四边形ABCD中，∠D=∠BCD=90°，∠B=60°，AB=6，AD=9，点E是CD上的一个动点（E不与D重合），过点E作EF∥AC，交AD于点F（当E运动到C时，EF与AC重合），把△DEF沿着EF对折，点D的对应点是点G．设DE=x，△GEF与四边形ABCD重叠部分的面积为y．

(1)、求CD的长及∠1的度数；

(2)、若点G恰好在BC上，求此时x的值；

(3)、求y与x之间的函数关系式，并求x为何值时，y的值最大？最大值是多少？

查看试题解析