2016年北京市大兴区中考数学一模试卷

试卷更新日期：2017-01-18 类型：中考模拟

进入出卷网下载

一、选择题

1. 北京新国际机场采用“海星”设计方案，航站楼主体与五座向外伸展的指廊总建筑面积为1 030 000平方米，将1030000用科学记数法表示应为（）

A、103×10⁴ B、10.3×10⁵ C、1.03×10⁵ D、1.03×10⁶

查看试题解析
2. 实数a，b，c，d在数轴上的对应点的位置如图所示，这四个数中，绝对值最小的是（）

A、a B、b C、c D、d

查看试题解析
3. 下列各图中，为中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 若正多边形的一个内角是120°，则这个正多边形的边数为（）

A、8 B、7 C、6 D、5

查看试题解析
5. 如图，AB∥CD，∠B=56°，∠E=22°，则∠D的度数为（）

A、22° B、34° C、56° D、78°

查看试题解析
6. 某班派9名同学参加红五月歌咏比赛，他们的身高分别是（单位：厘米）：167，159，161，159，163，157，170，159，165．这组数据的众数和中位数分别是（）

A、159，163 B、157，161 C、159，159 D、159，161

查看试题解析
7. 把多项式x³﹣xy²分解因式，下列结果正确的是（　　）

A、x（x+y）² B、x（x﹣y）² C、x（x﹣y）（x+y） D、x（x²﹣y²）

查看试题解析
8. 如图，AB是⊙O直径，弦CD⊥AB于点E．若CD=6，OE=4，则⊙O的直径为（）

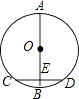A、5 B、6 C、8 D、10

查看试题解析
9. 如图，若在象棋盘上建立直角坐标系xOy，使“帥”位于点（﹣1，﹣2），“馬”位于点（2，﹣2），则“炮”位于点（）

A、（﹣2，﹣1） B、（0，0） C、（1，﹣2） D、（﹣1，1）

查看试题解析
10.
在五边形ABCDE中，∠B=90°，AB=BC=CD=1，AB∥CD，M是CD边的中点，点P由点A出发，按A→B→C→M的顺序运动．设点P经过的路程x为自变量，△APM的面积为y，则函数y的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若（m+2）²+ $\sqrt{n - 3}$ =0，则m﹣n= ．

查看试题解析
12. 半径为6cm，圆心角为40°的扇形的面积为 cm² ．

查看试题解析
13. 将函数y=x²﹣2x+4化为y=a（x﹣h）²+k的形式为．

查看试题解析
14. 一个不透明的盒子中装有2个白球，5个红球和3个黄球，这些球除颜色外，没有任何其它区别，现从这个盒子中随机摸出一个球，摸到红球的概率为．

查看试题解析
15. △ABC中，AB=AC，∠A=30°，以B为圆心，BC长为半径画弧，分别交AC，AB于D，E两点，并连结BD，DE．则∠BDE的度数为．

查看试题解析
16. 《九章算术》中记载：“今有竹高一丈，未折抵地，去根三尺，问折者高几何？”译文：有一根竹子原高一丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？我们用线段OA和线段AB来表示竹子，其中线段AB表示竹子折断部分，用线段OB表示竹梢触地处离竹根的距离，则竹子折断处离地面的高度OA是尺．

查看试题解析

三、解答题

17. 计算： $\sqrt{8}$ ﹣（ $\sqrt{3}$ ﹣1）⁰+（ $\frac{1}{2}$ ）^﹣²﹣4sin45°．

查看试题解析
18. 已知a是一元二次方程x²+3x﹣2=0的实数根，求代数式 $\frac{a - 3}{a^{2} - 2 a} \div (a + 2 - \frac{5}{a - 2})$ 的值．

查看试题解析
19. 解不等式 $\frac{2 x - 1}{3}$ ﹣ $\frac{5 x + 1}{2}$ ≥1，并把它的解集在数轴上表示出来．

查看试题解析
20. 已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点F．
求证：BF=AC．

查看试题解析
21. 列方程或方程组解应用题：
某校师生开展读书活动．九年级一班和九年级二班的学生向学校图书馆借课外读物共196本，一班每位学生借3本，二班每位学生借2本，一班借的课外读物数量比二班借的课外读物数量多44本，求九年级一班和二班各有学生多少人？

查看试题解析
22. 在▱ABCD中，过点D作对DE⊥AB于点E，点F在边CD上，CF=AE，连结AF，BF．

(1)、求证：四边形BFDE是矩形．

(2)、若CF=6，BF=8，DF=10，求证：AF是∠DAB的角平分线．

查看试题解析
23. 已知：如图，一次函数 $y = \frac{\sqrt{3}}{3} x + m$ 与反比例函数 $y = \frac{\sqrt{3}}{x}$ 的图象在第一象限的交点为A（1，n）．

(1)、求m与n的值；

(2)、设一次函数的图象与x轴交于点B，连结OA，求∠BAO的度数．

查看试题解析
24.
如图，已知AB是⊙O的直径，点H在⊙O上，E是 $\hat{H B}$ 的中点，过点E作EC⊥AH，交AH的延长线于点C．连接AE，过点E作EF⊥AB于点F．

(1)、求证：CE是⊙O的切线；

(2)、若FB=2，tan∠CAE= $\frac{\sqrt{2}}{2}$ ，求OF的长．

查看试题解析
25. 为了更好地贯彻落实国家关于“强化体育课和课外锻炼，促进青少年身心健康、体魄强健”的精神，某校大力开展体育活动．该校九年级三班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组．经调查，全班同学全员参与，各活动小组人数分布情况的扇形图和条形图如下：

(1)、求该班学生人数；

(2)、请你补全条形图；

(3)、求跳绳人数所占扇形圆心角的度数．

查看试题解析
26.
研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定方法．我们给出如下定义：如图，四边形ABCD中，AB=AD，CB=CD像这样两组邻边分别相等的四边形叫做“筝形”；

(1)、小文认为菱形是特殊的“筝形”，你认为他的判断正确吗？

(2)、小文根据学习几何图形的经验，通过观察、实验、归纳、类比、猜想、证明等方法，对AB≠BC的“筝形”的性质和判定方法进行了探究．下面是小文探究的过程，请补充完成：
①他首先发现了这类“筝形”有一组对角相等，并进行了证明，请你完成小文的证明过程．
已知：如图，在”筝形”ABCD中，AB=AD，CB=CD．
求证：∠ABC=∠ADC．
证明：②小文由①得到了这类“筝形”角的性质，他进一步探究发现这类“筝形”还具有其它性质，请再写出这类“筝形”的一条性质（除“筝形”的定义外）；
③继性质探究后，小文探究了这类“筝形”的判定方法，写出这类“筝形”的一条判定方法（除“筝形”的定义外）：

查看试题解析
27. 抛物线y₁=mx²+（m﹣3）x﹣3（m＞0）与x轴交于A、B两点，且点A在点B的左侧，与y轴交于点C，OB=OC．

(1)、求这条抛物线的表达式；

(2)、将抛物线y₁向左平移n（n＞0）个单位，记平移后y随着x的增大而增大的部分为P，若点C在直线y₂=﹣3x+t上，直线y₂向下平移n个单位，当平移后的直线与P有公共点时，求n的取值范围．

查看试题解析
28.
已知正方形ABCD，E为平面内任意一点，连结DE，将线段DE绕点D顺时针旋转90°得到DG，连结EC，AG．

(1)、当点E在正方形ABCD内部时，
①依题意补全图形；
②判断AG与CE的数量关系与位置关系并写出证明思路．

(2)、当点B，D，G在一条直线时，若AD=4，DG= $\sqrt{2}$ ，求CE的长．

查看试题解析
29.
设在一个变化过程中有两个变量x与y，如果对于x的每一个值，y都有唯一确定的值和它对应，那么就说y是x的函数，记作y=f（x）．在函数y=f（x）中，当自变量x=a时，相应的函数值y可以表示为f（a）．
例如：函数f（x）=x²﹣2x﹣3，当x=4时，f（4）=4²﹣2×4﹣3=5在平面直角坐标系xOy中，对于函数的零点给出如下定义：
如果函数y=f（x）在a≤x≤b的范围内对应的图象是一条连续不断的曲线，并且f（a）．f（b）＜0，那么函数y=f（x）在a≤x≤b的范围内有零点，即存在c（a≤c≤b），使f（c）=0，则c叫做这个函数的零点，c也是方程f（x）=0在a≤x≤b范围内的根．
例如：二次函数f（x）=x²﹣2x﹣3的图象如图1所示．

观察可知：f（﹣2）＞0，f（1）＜0，则f（﹣2）．f（1）＜0．所以函数f（x）=x²﹣2x﹣3在﹣2≤x≤1范围内有零点．由于f（﹣1）=0，所以，﹣1是f（x）=x²﹣2x﹣3的零点，﹣1也是方程x²﹣2x﹣3=0的根．

(1)、观察函数y₁=f（x）的图象2，回答下列问题：
①f（a）•f（b） 0（“＜”“＞”或“=”）
②在a≤x≤b范围内y₁=f（x）的零点的个数是．

(2)、已知函数y₂=f（x）=﹣ $\sqrt{3} x^{2} - 2 \sqrt{3} (a - 1) x - \sqrt{3} (a^{2} - 2 a)$ 的零点为x₁ ， x₂ ，且x₁＜1＜x₂ ．
①求零点为x₁ ， x₂（用a表示）；
②在平面直角坐标xOy中，在x轴上A，B两点表示的数是零点x₁ ， x₂ ，点 P为线段AB上的一个动点（P点与A、B两点不重合），在x轴上方作等边△APM和等边△BPN，记线段MN的中点为Q，若a是整数，求抛物线y₂的表达式并直接写出线段PQ长的取值范围．

查看试题解析