山东省滨州市2018年中考数学试卷
试卷更新日期:2018-06-29 类型:中考真卷
一、单选题
-
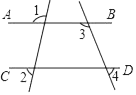
1. 在直角三角形中,若勾为3,股为4,则弦为( )A、5 B、6 C、7 D、82. 若数轴上点A、B分别表示数2、﹣2,则A、B两点之间的距离可表示为( )A、2+(﹣2) B、2﹣(﹣2) C、(﹣2)+2 D、(﹣2)﹣23. 如图,直线AB∥CD,则下列结论正确的是( )
 A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°4. 下列运算:①a2•a3=a6 , ②(a3)2=a6 , ③a5÷a5=a,④(ab)3=a3b3 , 其中结果正确的个数为( )A、1 B、2 C、3 D、45. 把不等式组 中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°4. 下列运算:①a2•a3=a6 , ②(a3)2=a6 , ③a5÷a5=a,④(ab)3=a3b3 , 其中结果正确的个数为( )A、1 B、2 C、3 D、45. 把不等式组 中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、 B、
B、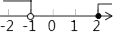 C、
C、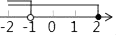 D、
D、 6. 在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的 后得到线段CD,则点A的对应点C的坐标为( )A、(5,1) B、(4,3) C、(3,4) D、(1,5)7. 下列命题,其中是真命题的为( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、一组邻边相等的矩形是正方形8. 已知半径为5的⊙O是△ABC的外接圆,若∠ABC=25°,则劣弧
6. 在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的 后得到线段CD,则点A的对应点C的坐标为( )A、(5,1) B、(4,3) C、(3,4) D、(1,5)7. 下列命题,其中是真命题的为( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、一组邻边相等的矩形是正方形8. 已知半径为5的⊙O是△ABC的外接圆,若∠ABC=25°,则劣弧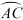 的长为( ) A、 B、 C、 D、9. 如果一组数据6、7、x、9、5的平均数是2x,那么这组数据的方差为( )A、4 B、3 C、2 D、110. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是( )
的长为( ) A、 B、 C、 D、9. 如果一组数据6、7、x、9、5的平均数是2x,那么这组数据的方差为( )A、4 B、3 C、2 D、110. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是( )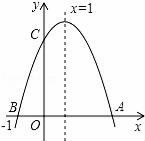 A、1 B、2 C、3 D、411. 如图,∠AOB=60°,点P是∠AOB内的定点且OP= ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
A、1 B、2 C、3 D、411. 如图,∠AOB=60°,点P是∠AOB内的定点且OP= ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )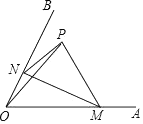 A、 B、 C、6 D、312. 如果规定[x]表示不大于x的最大整数,例如[2.3]=2,那么函数y=x﹣[x]的图象为( )A、
A、 B、 C、6 D、312. 如果规定[x]表示不大于x的最大整数,例如[2.3]=2,那么函数y=x﹣[x]的图象为( )A、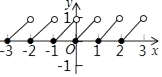 B、
B、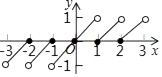 C、
C、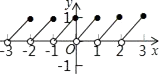 D、
D、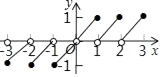
二、填空题
-
13. 在△ABC中,若∠A=30°,∠B=50°,则∠C= .14. 若分式 的值为0,则x的值为 .15. 在△ABC中,∠C=90°,若tanA= ,则sinB= .16. 若从﹣1,1,2这三个数中,任取两个分别作为点M的横、纵坐标,则点M在第二象限的概率是 .17. 若关于x、y的二元一次方程组 ,的解是 ,则关于a、b的二元一次方程组 的解是 .18. 若点A(﹣2,y1)、B(﹣1,y2)、C(1,y3)都在反比例函数y= (k为常数)的图象上,则y1、y2、y3的大小关系为 .19. 如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ,∠EAF=45°,则AF的长为 .
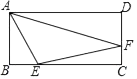 20. 观察下列各式:
20. 观察下列各式:,
,
,
……
请利用你所发现的规律,
计算 + + +…+ ,其结果为 .
三、解答题
-
21. 先化简,再求值:(xy2+x2y)× ,其中x=π0﹣( )﹣1 , y=2sin45°﹣ .22. 如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D,且AC平分∠DAB,求证:
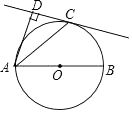 (1)、直线DC是⊙O的切线;(2)、AC2=2AD•AO.23. 如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题:
(1)、直线DC是⊙O的切线;(2)、AC2=2AD•AO.23. 如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题: (1)、在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?(2)、在飞行过程中,小球从飞出到落地所用时间是多少?(3)、在飞行过程中,小球飞行高度何时最大?最大高度是多少?24. 如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1, ).
(1)、在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?(2)、在飞行过程中,小球从飞出到落地所用时间是多少?(3)、在飞行过程中,小球飞行高度何时最大?最大高度是多少?24. 如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1, ).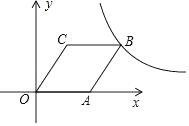 (1)、求图象过点B的反比例函数的解析式;(2)、求图象过点A,B的一次函数的解析式;
(1)、求图象过点B的反比例函数的解析式;(2)、求图象过点A,B的一次函数的解析式;
(3)、在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.25. 已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.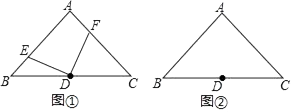 (1)、如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;(2)、若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.26. 如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)、如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;(2)、若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.26. 如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.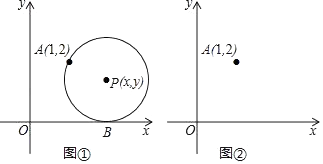 (1)、当x=2时,求⊙P的半径;(2)、求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;(3)、请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到的距离等于到的距离的所有点的集合.(4)、当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
(1)、当x=2时,求⊙P的半径;(2)、求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;(3)、请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到的距离等于到的距离的所有点的集合.(4)、当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.