山东省德州市2018年中考数学试卷
试卷更新日期:2018-06-29 类型:中考真卷
一、单选题
-
1. 3的相反数是( )A、 3 B、 C、-3 D、2. 下列图形中,既是轴对称又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.496亿 .用科学记数法表示1.496亿是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 已知一组数据:6,2,8, ,7,它们的平均数是6.则这组数据的中位数是( )A、7 B、6 C、5 D、46. 如图,将一副三角尺按不同的位置摆放,下列摆放方式中 与 互余的是( )
3. 一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.496亿 .用科学记数法表示1.496亿是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 已知一组数据:6,2,8, ,7,它们的平均数是6.则这组数据的中位数是( )A、7 B、6 C、5 D、46. 如图,将一副三角尺按不同的位置摆放,下列摆放方式中 与 互余的是( )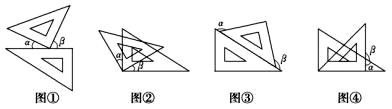 A、图① B、图② C、图③ D、图④7. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、
A、图① B、图② C、图③ D、图④7. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、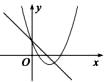 B、
B、 C、
C、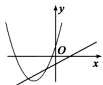 D、
D、 8. 分式方程 的解为( )A、 B、 C、 D、无解9. 如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )
8. 分式方程 的解为( )A、 B、 C、 D、无解9. 如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )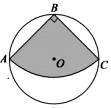 A、 B、 C、 D、10. 给出下列函数:①y=﹣3x+2;②y= ;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是( )A、①③ B、③④ C、②④ D、②③11. 我国南宋数学家杨辉所著的《详解九章算术》一书中,用下图的三角形解释二项式
A、 B、 C、 D、10. 给出下列函数:①y=﹣3x+2;②y= ;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是( )A、①③ B、③④ C、②④ D、②③11. 我国南宋数学家杨辉所著的《详解九章算术》一书中,用下图的三角形解释二项式的展开式的各项系数,此三角形称为“杨辉三角”.
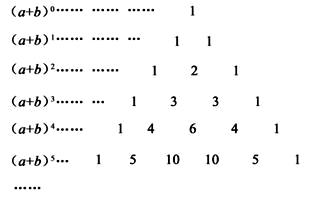
根据“杨辉三角”请计算 的展开式中从左起第四项的系数为( )
A、84 B、56 C、35 D、2812. 如图,等边三角形 的边长为4,点 是△ 的中心, .绕点 旋转 ,分别交线段 于D、E两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于 ;④△ 周长的最小值为6,上述结论中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 计算: = .14. 若 x1、x2是一元二次方程 的两个实数根,则 = .
15. 如图, 为 的平分线. , . .则点 到射线 的距离为 .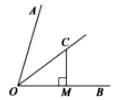 16. 如图。在 的正方形方格图形中,小正方形的顶点称为格点. 的顶点都在格点上,则 的正弦值是 .
16. 如图。在 的正方形方格图形中,小正方形的顶点称为格点. 的顶点都在格点上,则 的正弦值是 . 17. 对于实数a,b,定义运算“◆”:a◆b= ,例如4◆3,因为4>3.所以4◆3= =5.若x,y满足方程组 ,则x◆y=.18. 如图,反比例函数 与一次函数 在第三象限交于点 .点 的坐标为(一3,0),点 是 轴左侧的一点.若以 为顶点的四边形为平行四边形.则点 的坐标为.
17. 对于实数a,b,定义运算“◆”:a◆b= ,例如4◆3,因为4>3.所以4◆3= =5.若x,y满足方程组 ,则x◆y=.18. 如图,反比例函数 与一次函数 在第三象限交于点 .点 的坐标为(一3,0),点 是 轴左侧的一点.若以 为顶点的四边形为平行四边形.则点 的坐标为.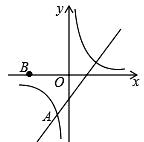
三、解答题
-
19. 先化简,再求值: ,其中 是不等式组 的整数解.20. 某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)、这次被调查的学生共有多少人?
(2)、请将条形统计图补充完整;(3)、若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?(4)、该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)21. 如图,两座建筑物的水平距离 为 .从 点测得 点的仰角 为53° ,从 点测得 点的俯角 为37° ,求两座建筑物的高度(参考数据: 22. 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
22. 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.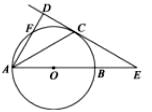 (1)、求证:AD⊥CD;(2)、若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14, ≈1.73,结果保留一位小数.)23. 为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价 (单位:万元)成一次函数关系.
(1)、求证:AD⊥CD;(2)、若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14, ≈1.73,结果保留一位小数.)23. 为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价 (单位:万元)成一次函数关系.
(1)、求年销售量 与销售单价 的函数关系式;(2)、根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?24. 再读教材:宽与长的比是 (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; )
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
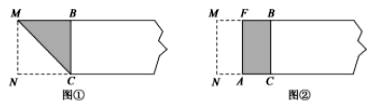
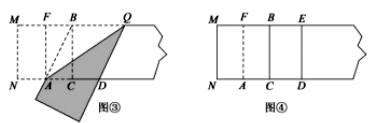
第三步,折出内侧矩形的对角线 ,并把 折到图③中所示的 处,
第四步,展平纸片,按照所得的点 折出 ,使 ,则图④中就会出现黄金矩形,
问题解决:
(1)、图③中 =(保留根号);(2)、如图③,判断四边形 的形状,并说明理由;(3)、请写出图④中所有的黄金矩形,并选择其中一个说明理由.(4)、结合图④.请在矩形 中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.25. 如图1,在平面直角坐标系中,直线 与抛物线 交于 两点,其中 , .该抛物线与 轴交于点 ,与 轴交于另一点 .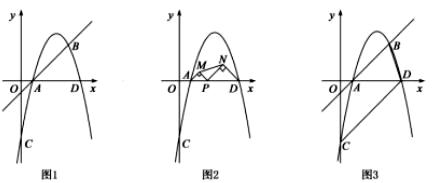 (1)、求 的值及该抛物线的解析式;(2)、如图2.若点 为线段 上的一动点(不与 重合).分别以 、 为斜边,在直线 的同侧作等腰直角△ 和等腰直角△ ,连接 ,试确定△ 面积最大时 点的坐标.(3)、如图3.连接 、 ,在线段 上是否存在点 ,使得以 为顶点的三角形与△ 相似,若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求 的值及该抛物线的解析式;(2)、如图2.若点 为线段 上的一动点(不与 重合).分别以 、 为斜边,在直线 的同侧作等腰直角△ 和等腰直角△ ,连接 ,试确定△ 面积最大时 点的坐标.(3)、如图3.连接 、 ,在线段 上是否存在点 ,使得以 为顶点的三角形与△ 相似,若存在,请直接写出点 的坐标;若不存在,请说明理由.