四川省宜宾市2018年中考数学试卷
试卷更新日期:2018-06-29 类型:中考真卷
一、选择题:
-
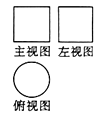
1. 3的相反数是( )A、 B、3 C、 D、2. 我国首艘国产航母于2018年4月26日正式下水,排水量为65000吨.将65000用科学记数法表示为( )A、 B、 C、 D、3. 一个立体图形的三视图如图所示,则该立体图形是( )
 A、圆柱 B、圆锥 C、长方体 D、球4. 一元二次方程 的两根分别为 和 ,则 为( )A、 B、1 C、2 D、05. 在 中,若 与 的角平分线交于点 ,则 的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定6. 某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019年“竹文化”旅游输入将达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )A、 B、 C、 D、7. 如图,将 沿 边上的中线 平移到 的位置,已知 的面积为9,阴影部分三角形的面积为4.若 ,则 等于( )
A、圆柱 B、圆锥 C、长方体 D、球4. 一元二次方程 的两根分别为 和 ,则 为( )A、 B、1 C、2 D、05. 在 中,若 与 的角平分线交于点 ,则 的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定6. 某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019年“竹文化”旅游输入将达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )A、 B、 C、 D、7. 如图,将 沿 边上的中线 平移到 的位置,已知 的面积为9,阴影部分三角形的面积为4.若 ,则 等于( ) A、2 B、3 C、 D、8. 在 中,若 为 边的中点,则必有 成立.依据以上结论,解决如下问题:如图,在矩形 中,已知 ,点 在以 为直径的半圆上运动,则 的最小值为( )
A、2 B、3 C、 D、8. 在 中,若 为 边的中点,则必有 成立.依据以上结论,解决如下问题:如图,在矩形 中,已知 ,点 在以 为直径的半圆上运动,则 的最小值为( )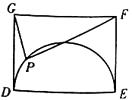 A、 B、 C、34 D、10
A、 B、 C、34 D、10二、填空题
-
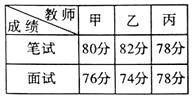
9. 分解因式: .10. 不等式组 的所有整数解的和为.11. 某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示.综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,则被录取教师的综合成绩为分.
 12. 已知点 是直线 上一点,其横坐标为 .若点 与点 关于 轴对称,则点 的坐标为.13. 刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.设⊙ 的半径为1,若用⊙ 的外切正六边形的面积 来近似估计⊙ 的面积,则 .(结果保留根号)14. 已知点 在直线 上,也在双曲线 上,则 的值为.15. 如图, 是半圆的直径, 是一条弦, 是的中点, 于点 且 交 于点 , 交 于点 .若 ,则 .
12. 已知点 是直线 上一点,其横坐标为 .若点 与点 关于 轴对称,则点 的坐标为.13. 刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.设⊙ 的半径为1,若用⊙ 的外切正六边形的面积 来近似估计⊙ 的面积,则 .(结果保留根号)14. 已知点 在直线 上,也在双曲线 上,则 的值为.15. 如图, 是半圆的直径, 是一条弦, 是的中点, 于点 且 交 于点 , 交 于点 .若 ,则 . 16. 如图,在矩形 中, ,点 为线段 上的动点,将 沿 折叠,使点 落在矩形内点 处.下列结论正确的是. (写出所有正确结论的序号)
16. 如图,在矩形 中, ,点 为线段 上的动点,将 沿 折叠,使点 落在矩形内点 处.下列结论正确的是. (写出所有正确结论的序号)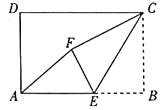
①当 为线段 中点时, ;
②当 为线段 中点时, ;
③当 三点共线时, ;
④当 三点共线时, .
三、解答题
-
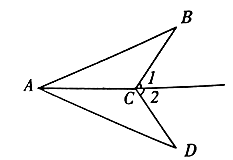
17.(1)、计算: ;(2)、化简: .18. 如图,已知 ,求证: .
 19. 某高中进行“选科走班”教学改革,语文、数学、英语三门为必修学科,另外还需从物理、化学、生物、政治、历史、地理(分别记为 )六门选修学科中任选三门.现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.
19. 某高中进行“选科走班”教学改革,语文、数学、英语三门为必修学科,另外还需从物理、化学、生物、政治、历史、地理(分别记为 )六门选修学科中任选三门.现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.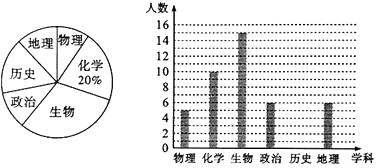
请根据以上信息,完成下列问题:
(1)、该班共有学生人;(2)、请将条形统计图补充完整;(3)、该班某同学物理成绩特别优异,已经从选修学科中选定物理,还需从余下选修学科中任意选择两门.请用列表或画树状图的方法,求出该同学恰好选中化学、历史两科的概率.20. 我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际 每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货.求每月实际生产智能手机多少万部.21. 某游乐场一转角滑梯如图所示,滑梯立柱 均垂直于地面,点 在线段 上.在 点测得点 的仰角为 ,点 的俯角也为 ,测得 间的距离为10米,立柱 高30米.求立柱 的高(结果保留根号).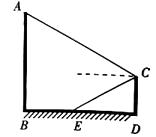 22. 如图,已知反比例函数 的图象经过点 ,一次函数 的图象经过反比例函数图象上的点 .
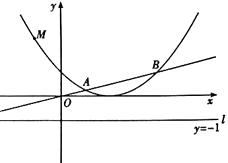
22. 如图,已知反比例函数 的图象经过点 ,一次函数 的图象经过反比例函数图象上的点 .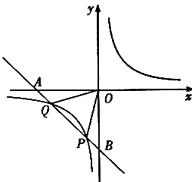 (1)、求反比例函数与一次函数的表达式;(2)、一次函数的图象分别与 轴、 轴交于 两点,与反比例函数图象的另一个交点为 ,连结 .求 的面积.
(1)、求反比例函数与一次函数的表达式;(2)、一次函数的图象分别与 轴、 轴交于 两点,与反比例函数图象的另一个交点为 ,连结 .求 的面积.