广东省深圳市2018年中考数学试卷

试卷更新日期：2018-06-26 类型：中考真卷

进入出卷网下载

一、选择题

1. 6的相反数是（）

A、 $- 6$ B、 $- \frac{1}{6}$ C、 $\frac{1}{6}$ D、6

查看试题解析
2. 260000000用科学记数法表示为（）

A、 $0.26 \times 10^{9}$ B、 $2.6 \times 10^{8}$ C、 $2.6 \times 10^{9}$ D、 $26 \times 10^{7}$

查看试题解析
3. 图中立体图形的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 观察下列图形，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 下列数据： $75 ， 80 ， 85 ， 85 ， 85$ ，则这组数据的众数和极差是（）

A、 $85 ， 10$ B、 $85 ， 5$ C、 $80 ， 85$ D、 $80 ， 10$

查看试题解析
6. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $3 a - a = 2 a$ C、 $a^{8} \div a^{4} = a^{2}$ D、 $\sqrt{a} + \sqrt{b} = \sqrt{a b}$

查看试题解析
7. 把函数y=x向上平移3个单位，下列在该平移后的直线上的点是（）

A、 $(2 ， 2)$ B、 $(2 ， 3)$ C、 $(2 ， 4)$ D、 $(2 ， 5)$

查看试题解析
8. 如图，直线 $a ， b$ 被 $c ， d$ 所截，且 $a / / b$ ，则下列结论中正确的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ 2 + ∠ 4 = 180^{\circ}$ D、 $∠ 1 + ∠ 4 = 180^{\circ}$

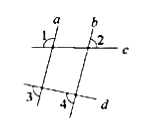查看试题解析
9. 某旅店一共70个房间，大房间每间住8个人，小房间每间住6个人，一共480个学生刚好住满，设大房间有 $x$ 个，小房间有 $y$ 个.下列方程正确的是（）

A、 ${\begin{matrix} x + y = 70 \\ 8 x + 6 y = 480 \end{matrix}$ B、 ${\begin{matrix} x + y = 70 \\ 6 x + 8 y = 480 \end{matrix}$ C、 ${\begin{matrix} x + y = 480 \\ 6 x + 8 y = 70 \end{matrix}$ D、 ${\begin{matrix} x + y = 480 \\ 8 x + 6 y = 70 \end{matrix}$

查看试题解析
10. 如图，一把直尺， 60°的直角三角板和光盘如图摆放， A为 60°角与直尺交点， AB=3 ，则光盘的直径是（）

A、3 B、 $3 \sqrt{3}$ C、 $6$ D、 $6 \sqrt{3}$

查看试题解析
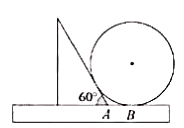11. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像如图所示，下列结论正确的是（）

A、 $a b c > 0$ B、 $2 a + b < 0$ C、 $3 a + c < 0$ D、 $a x^{2} + b x + c - 3 = 0$ 有两个不相等的实数根

查看试题解析
12. 如图， $A 、 B$ 是函数 $y = \frac{12}{x}$ 上两点， $P$ 为一动点，作 $P B / / y$ 轴， $P A / / x$ 轴，下列说法正确的是（）
① $Δ A O P ≅ Δ B O P$ ；② $S_{Δ A O P} = S_{Δ B O P}$ ；③若 $O A = O B$ ，则 $O P$ 平分 $∠ A O B$ ；④若 $S_{Δ B O P} = 4$ ，则 $S_{Δ A B P} = 16$

A、①③ B、②③ C、②④ D、③④

查看试题解析

二、填空题

13. 分解因式： $a^{2} - 9 =$ ．

查看试题解析
14. 一个正六面体的骰子投掷一次得到正面向上的数字为奇数的概率．

查看试题解析
15. 如图，四边形ACFD是正方形，∠CEA和∠ABF都是直角且点E、A、B三点共线，AB=4，则阴影部分的面积是．

查看试题解析
16. 在Rt△ABC中∠C=90°，AD平分∠CAB，BE平分∠CBA，AD、BE相交于点F，且AF=4，EF= $\sqrt{2}$ ，则AC= ．

查看试题解析

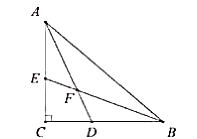
三、解答题

17. 计算： ${(\frac{1}{2})}^{-1} - 2 \sin 45^{\circ} + | \sqrt{2} | +(2018- π)^{0}$ .

查看试题解析
18. 先化简，再求值： $(\frac{x}{x - 1} - 1) \div \frac{x^{2} + 2 x + 1}{x^{2} - 1}$ ，其中 $x = 2$ .

查看试题解析
19. 某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计图：

频数
频率
体育
40
0.4
科技
25
$a$
艺术
$b$
0.15
其它
20
0.2

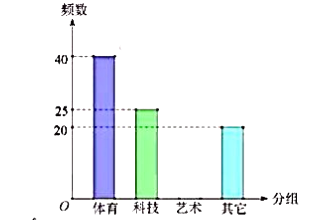
请根据上图完成下面题目：

(1)、总人数为人， $a =$ ， $b =$ .

(2)、请你补全条形统计图.

(3)、若全校有600人，请你估算一下全校喜欢艺术类学生的人数有多少？

查看试题解析
20. 已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于 $\frac{1}{2}$ AD长为半径做弧，交 $E F$ 于点B，AB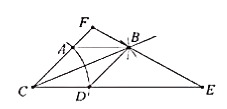∥CD.

(1)、求证：四边形ACDB为△CFE的亲密菱形；

(2)、求四边形ACDB的面积.

查看试题解析
21. 某超市预测某饮料有发展前途，用1600元购进一批饮料，面市后果然供不应求，又用6000元购进这批饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元.

(1)、第一批饮料进货单价多少元？

(2)、若二次购进饮料按同一价格销售，两批全部售完后，获利不少于1200元，那么销售单价至少为多少元？

查看试题解析
22. 如图：在 $⊙ O$ 中，BC=2，AB=AC，点D为AC上的动点，且 $\cos B = \frac{\sqrt{10}}{10}$ .

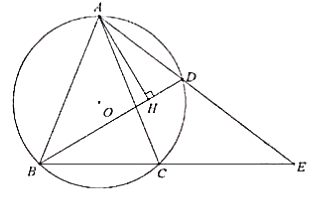(1)、求AB的长度；

(2)、求AD·AE的值；

(3)、过A点作AH⊥BD，求证：BH=CD+DH.

查看试题解析
23. 已知顶点为 $A$ 抛物线 $y = a {(x - \frac{1}{2})}^{2} - 2$ 经过点 $B (- \frac{3}{2} ， 2)$ ，点 $C (\frac{5}{2} ， 2)$ .

(1)、求抛物线的解析式；

(2)、如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠OPM=∠MAF，求△POE的面积；

(3)、如图2，点Q是折线A-B-C上一点，过点Q作QN∥y轴，过点E作EN∥x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN₁ ，若点N₁落在x轴上，请直接写出Q点的坐标.

查看试题解析

	频数	频率
体育	40	0.4
科技	25	$a$
艺术	$b$	0.15
其它	20	0.2