2016-2017学年山东省日照市莒县八年级上学期期中数学试卷

试卷更新日期：2017-01-16 类型：期中考试

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、x²+x²=x⁴ B、（a﹣b）²=a²﹣b² C、（﹣a²）³=﹣a⁶ D、3a²•2a³=6a⁶

查看试题解析
2. 在 $\frac{1}{x}$ , $\frac{1}{2}$ , $\frac{x^{2} + 1}{2}$ , $\frac{3 x y}{π}$ , $\frac{3}{x + y}$ ,a+ $\frac{1}{m}$ 中，分式的个数是（　　）

A、2 B、3 C、4 D、5

查看试题解析
3. 已知等腰三角形的一个内角为70°，则另两个内角的度数是（）

A、55°，55° B、70°，40° C、55°，55°或70°，40° D、以上都不对

查看试题解析
4. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为零，则x的值是（）

A、±1 B、1 C、﹣1 D、0

查看试题解析
5. 如果x²+10x+（）=（x+5）² ，括号处填（）

A、5 B、10 C、25 D、±10

查看试题解析
6. 把多项式x²+ax+b分解因式，得（x+1）（x﹣3）则a，b的值分别是（）

A、a=2，b=3 B、a=﹣2，b=﹣3 C、a=﹣2，b=3 D、a=2，b=﹣3

查看试题解析
7.
在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），再沿虚线剪开，如图（1），然后拼成一个梯形，如图（2），根据这两个图形的面积关系，表明下列式子成立的是（　　）

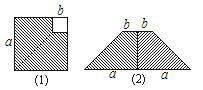A、a²﹣b²=（a+b）（a﹣b） B、（a+b）²=a²+2ab+b² C、（a﹣b）²=a²﹣2ab+b² D、a²﹣b²=（a﹣b）²

查看试题解析
8. 分式 $\frac{2 x^{2}}{3 x - 2 y}$ 中的x，y同时扩大2倍，则分式的值（）

A、不变 B、是原来的2倍 C、是原来的4倍 D、是原来的 $\frac{1}{2}$

查看试题解析
9. 已知10^m=2，10ⁿ=3，则10^3m⁺²ⁿ=（）

A、17 B、72 C、12 D、36

查看试题解析
10. 观察下列各式及其展开式：
（a+b）²=a²+2ab+b²
（a+b）³=a³+3a²b+3ab²+b³
（a+b）⁴=a⁴+4a³b+6a²b²+4ab³+b⁴
（a+b）⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵
…
请你猜想（a+b）¹⁰的展开式第三项的系数是（）

A、36 B、45 C、55 D、66

查看试题解析
11. 在平面直角坐标系xOy中，已知点A（2，﹣2），在坐标轴上确定点P，使△AOP为等腰三角形，则符合条件的有（）个．

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

12. 把一张纸各按图中那样折叠后，若得到∠AOB′=70°，则∠BOG= ．

查看试题解析
13. 等腰三角形的周长是25cm，一腰上的中线将周长分为3：2两部分，则此三角形的底边长为 cm或 cm．

查看试题解析
14. 已知a²﹣a﹣1=0，则a³﹣a²﹣a+2016= ．

查看试题解析
15. 如图，已知点B．C．D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H．
①△BCE≌△ACD；
②CF=CH；
③△CFH为等边三角形；
④FH∥BD；
⑤AD与BE的夹角为60°，
以上结论正确的是．

查看试题解析

三、解答题

16. 计算：

(1)、（2×10⁵）÷（8×10^﹣⁵）

(2)、（x+y）²﹣（x+y）（x﹣y）

查看试题解析
17. 化简求值。

(1)、已知x+y=15，x²+y²=113，求x²﹣xy+y²的值．

(2)、先化简，再求值： $\frac{x^{2} - 4 x + 4}{2 x}$ ÷ $\frac{x^{2} - 2 x}{x^{2}}$ +1，在0，1，2，三个数中选一个合适的，代入求值．

查看试题解析
18. 平面直角坐标系中，△ABC的三个顶点坐标分别为A（0，4），B（3，4），C（4，﹣1）．

(1)、试在平面直角坐标系中，画出△ABC；

(2)、若△A₁B₁C₁与△ABC关于x轴对称，写出A₁、B₁、C₁的坐标；

(3)、在x轴上找到一点P，使点P到点A、B两点的距离和最小；

(4)、求△ABC的面积．

查看试题解析
19. 如图，AB=AC，CD⊥AB于点D，BE⊥AC于点E，BE与CD相交于点O．

(1)、求证：AD=AE；

(2)、试猜想：OA与BC的位置关系，并加以证明．

查看试题解析
20. 下面是某同学对多项式（x²﹣4x﹣3）（x²﹣4x+1）+4进行因式分解的过程．
解：设x²﹣4x=y
原式=（y﹣3）（y+1）+4（第一步）
=y²﹣2y+1 （第二步）
=（y﹣1）² （第三步）
=（x²﹣4x﹣1）²（第四步）
回答下列问题：

(1)、该同学第二步到第三步运用了因式分解的．

A、提取公因式法 B、平方差公式法 C、完全平方公式法

(2)、请你模仿以上方法尝试对多项式（x²+2x）（x²+2x+2）+1进行因式分解．

查看试题解析
21.
如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．

(1)、当∠BQD=30°时，求AP的长；

(2)、证明：在运动过程中，点D是线段PQ的中点；

(3)、当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．

查看试题解析