2016-2017学年江西省宜春市高安市八年级上学期期中数学试卷
试卷更新日期：2017-01-16 类型：期中考试
一、选择题
-
1. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 以下列每组长度的三条线段为边能组成三角形的是（ ）A、2、3、6 B、2、4、6 C、2、2、4 D、6、6、63. 一个多边形的每一个内角都等于140°，则它的边数是（ ）A、7 B、8 C、9 D、104. 如图，已知∠CAB=∠DAB，则添加下列一个条件不能使△ABC≌△ABD的是（ ）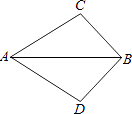
A、AC=AD B、BC=BD C、∠C=∠D D、∠ABC=∠ABD5. 如图，BE、CF是△ABC的角平分线，∠ABC=80°，∠ACB=60°，BE、CF相交于D，则∠CDE的度数是（ ）
A、60° B、70° C、80° D、50°6. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（ ）
A、10 B、7 C、5 D、4二、填空题
-
7. 点M（1，2）关于x轴对称的点的坐标为 ．8. 把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为
9. 如图：△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，则△ABC的周长为 ．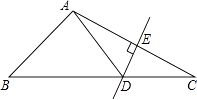
10. 如图，∠1+∠2+∠3+∠4+∠5+∠6=度．
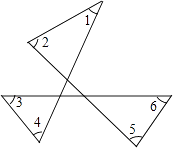11. 如图，已知∠AOB等于30°，角内有一点P，OP=6，点M在OA上，点N在OB上，△PMN周长的最小值是
12. 如图，在Rt△ABC中，∠C=90°，AC=16，BC=8，PQ=AB，点P和点Q分别在AC和AC的垂线AD上移动，则当AP=时，才能使△ABC和△APQ全等．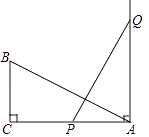
三、作图题
-
13. 作图题：（不写作法，但要保留痕迹）
在图中找出点A，使它到M，N两点的距离相等，并且到OH，OF的距离相等．
14. 如图，AD为△ABC的中线，BE为三角形ABD中线．
(1)、在△BED中作BD边上的高EH；(2)、若△ABC的面积为40，BD=5，求EH的长．15. 如图，点B、D、C、F在一条直线上，BC=FD，AB=EF，且AB∥EF．求证：AC∥ED．
16. 如果一个多边形的内角和是外角和的3倍还多180°，那么这个多边形的边数是多少？17. 如图，已知△ABC的三个顶点的坐标分别为A（﹣5，3）、B（﹣2，﹣2）、C（﹣3，4）．
(1)、作出△ABC关于y轴对称的△A1B1C1；(2)、写出点A关于x轴对称的点A2的坐标；(3)、△ABC的面积为 ．四、解答题
-
18. 两个大小不同的等腰直角三角形三角板如图①所示放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC，
(1)、请找出图②中的全等三角形，并给予说明（说明：结论中不得含有未标识的字母）；(2)、试说明：DC⊥BE．19. 如图所示，∠BAC=∠ABD，AC=BD，点O是AD、BC的交点，点E是AB的中点．试判断OE和AB的位置关系，并给出证明．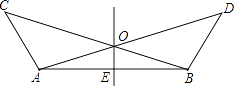
20. 如图，在等边三角形ABC中，点E、D分别从A、C出发，沿AC，CB方向以相同的速度在线段AC，CB上运动，AD、BE相交于F点．
(1)、求证：△ABE≌△CAD；(2)、当E、D运动时，∠BFD大小是否发生改变？若不变求其大小，若改变求其变化范围．21.阅读下面材料：
小聪遇到这样一个有关角平分线的问题：如图1，在△ABC中，∠A=2∠B，CD平分∠ACB，AD=2.2，AC=3.6
求BC的长．
小聪思考：因为CD平分∠ACB，所以可在BC边上取点E，使EC=AC，连接DE．这样很容易得到△DEC≌△DAC，经过推理能使问题得到解决（如图2）．
请回答：
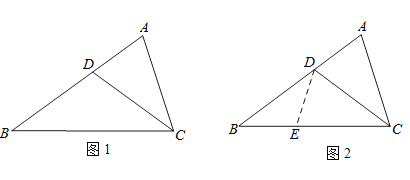(1)、△BDE是
(2)、BC的长为
22. 如图1，在Rt△ACB中，∠ACB=90°，∠ABC=30°，AC=1，点D为AC上一动点，连接BD，以BD为边作等边△BDE，设CD=n．
(1)、当n=1时，EA的延长线交BC的延长线于F，则AF=；(2)、当0＜n＜1时，如图2，在BA上截取BH=AD，连接EH．①设∠CBD=x，用含x的式子表示∠ADE和∠ABE．
②求证：△AEH为等边三角形．
23. 如图1，已知线段AC∥y轴，点B在第一象限，且AO平分∠BAC，AB交y轴与G，连OB、OC．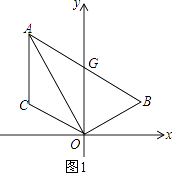
(1)、判断△AOG的形状，并予以证明；(2)、若点B、C关于y轴对称，求证：AO⊥BO；(3)、在（2）的条件下，如图2，点M为OA上一点，且∠ACM=45°，BM交y轴于P，若点B的坐标为（3，1），求点M的坐标．