2016-2017学年湖北省宜昌市八年级上学期期中数学试卷
试卷更新日期:2017-01-16 类型:期中考试
一、选择题
-
1. 若一个三角形的两边长分别为3和7,则第三边长可能是( )A、2 B、3 C、5 D、112. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )
A、 B、
B、 C、
C、 D、
D、 3. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、
3. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、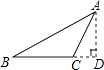 B、
B、 C、
C、 D、
D、 4. 如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
4. 如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( ) A、110° B、120° C、130° D、140°5. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
A、110° B、120° C、130° D、140°5. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( ) A、1个 B、2个 C、3个 D、4个6. 如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A、1个 B、2个 C、3个 D、4个6. 如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( ) A、AC=BD B、∠CAB=∠DBA C、∠C=∠D D、BC=AD7. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°8. 一个等腰三角形的两边长分别为4,8,则它的周长为( )A、12 B、16 C、20 D、16或209. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
A、AC=BD B、∠CAB=∠DBA C、∠C=∠D D、BC=AD7. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°8. 一个等腰三角形的两边长分别为4,8,则它的周长为( )A、12 B、16 C、20 D、16或209. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO= AC;③△ABD≌△CBD,
其中正确的结论有( )
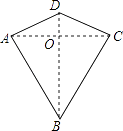 A、0个 B、1个 C、2个 D、3个10. 如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( )
A、0个 B、1个 C、2个 D、3个10. 如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( )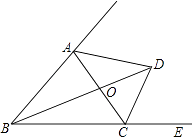 A、∠BAC=70° B、∠DOC=90° C、∠BDC=35° D、∠DAC=55°11. 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
A、∠BAC=70° B、∠DOC=90° C、∠BDC=35° D、∠DAC=55°11. 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( ) A、13 B、15 C、17 D、1912. 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A、13 B、15 C、17 D、1912. 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )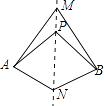 A、AM=BM B、AP=BN C、∠MAP=∠MBP D、∠ANM=∠BNM13. 如图,AD是△ABC的角平分线,则AB:AC等于( )
A、AM=BM B、AP=BN C、∠MAP=∠MBP D、∠ANM=∠BNM13. 如图,AD是△ABC的角平分线,则AB:AC等于( )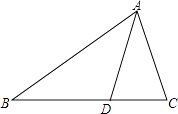 A、BD:CD B、AD:CD C、BC:AD D、BC:AC14. 如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( )
A、BD:CD B、AD:CD C、BC:AD D、BC:AC14. 如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、解答题
-
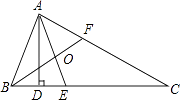
15. 如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=80°,∠ABC=70°.求∠BAD,∠AOF.
 16. 如图,AB=AD,CB=CD,求证:AC平分∠BAD.
16. 如图,AB=AD,CB=CD,求证:AC平分∠BAD.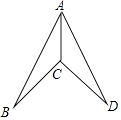 17. 如图,已知AC=AE,∠BAD=∠CAE,∠B=∠ADE,求证:BC=DE.
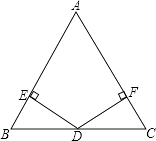
17. 如图,已知AC=AE,∠BAD=∠CAE,∠B=∠ADE,求证:BC=DE. 18. 如图,在△ABC中,AB=AC,点D是BC边上的中点,DE、DF分别垂直AB、AC于点E和F.
18. 如图,在△ABC中,AB=AC,点D是BC边上的中点,DE、DF分别垂直AB、AC于点E和F.求证:DE=DF.
 19. 如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由.
19. 如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由. 20. 如图,在等腰三角形ABC中,AC=BC,分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE,AE与BD相交于点F,连接CF并延长交AB于点G.求证:CG垂直平分AB.
20. 如图,在等腰三角形ABC中,AC=BC,分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE,AE与BD相交于点F,连接CF并延长交AB于点G.求证:CG垂直平分AB. 21. 如图,在等边△ABC中,点F是AC边上一点,延长BC到点D,使BF=DF,若CD=CF,求证:
21. 如图,在等边△ABC中,点F是AC边上一点,延长BC到点D,使BF=DF,若CD=CF,求证: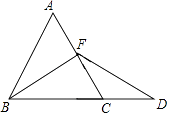 (1)、点F为AC的中点;(2)、过点F作FE⊥BD,垂足为点E,请画出图形并证明BD=6CE.22. 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)、点F为AC的中点;(2)、过点F作FE⊥BD,垂足为点E,请画出图形并证明BD=6CE.22. 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.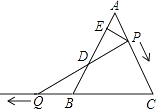 (1)、当∠BQD=30°时,求AP的长;(2)、当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.23. 在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是BC边上一点,BN⊥AD交AD的延长线于点N.
(1)、当∠BQD=30°时,求AP的长;(2)、当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.23. 在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是BC边上一点,BN⊥AD交AD的延长线于点N.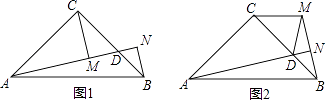 (1)、如图1,若CM∥BN交AD于点M.
(1)、如图1,若CM∥BN交AD于点M.①直接写出图1中所有与∠MCD相等的角:;(注:所找到的相等关系可以直接用于第②小题的证明过程
②过点C作CG⊥BN,交BN的延长线于点G,请先在图1中画出辅助线,再回答线段AM、CG、BN有怎样的数量关系,并给予证明 .
(2)、如图2,若CM∥AB交BN的延长线于点M.请证明:∠MDN+2∠BDN=180°.