浙江省义乌市2018年中考数学试卷
试卷更新日期:2018-06-26 类型:中考真卷
一、选择题
-
1. 如果向东走 记为 ,则向西走 可记为( )A、 B、 C、 D、2. 绿水青山就是金山银山,为了创造良好的生态生活环境,浙江省2017年清理河湖库塘淤泥约116000000方,数字116000000用科学记数法可以表示为( )A、 B、 C、 D、3. 有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )
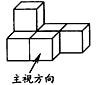 A、
A、 B、
B、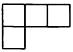 C、
C、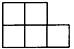 D、
D、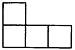 4. 抛掷一枚质地均匀的立方体骰子一次,骰子的六个面上分别标有数字1,2,3,4,5,6,则朝上一面的数字为2的概率是( )
4. 抛掷一枚质地均匀的立方体骰子一次,骰子的六个面上分别标有数字1,2,3,4,5,6,则朝上一面的数字为2的概率是( )
A、 B、 C、 D、5. 下面是一位同学做的四道题:① .② .③ .④ .其中做对的一道题的序号是( )A、① B、② C、③ D、④6. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则此函数( )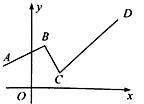 A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小7. 学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知 , ,垂足分别为 , , , , ,则栏杆 端应下降的垂直距离 为( )
A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小7. 学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知 , ,垂足分别为 , , , , ,则栏杆 端应下降的垂直距离 为( )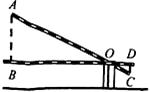 A、 B、 C、 D、8. 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
A、 B、 C、 D、8. 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 9. 若抛物线 与 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线 ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
9. 若抛物线 与 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线 ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A、 B、 C、 D、10. 某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合),现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图),若有34枚图钉可供选用,则最多可以展示绘画作品( )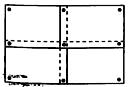 A、16张 B、18张 C、20张 D、21张
A、16张 B、18张 C、20张 D、21张二、填空题
-
11. 因式分解: .12. 我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托.如果1托为5尺,那么索长为尺,竿子长为尺.
13. 如图,公园内有一个半径为20米的圆形草坪, , 是圆上的点, 为圆心, ,从 到 只有路 ,一部分市民为走“捷径”,踩坏了花草,走出了一条小路 .通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数).(参考数据: , 取3.142)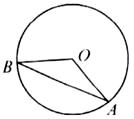 14. 等腰三角形 中,顶角 为 ,点 在以 为圆心, 长为半径的圆上,且 ,则 的度数为 .15. 过双曲线 的动点 作 轴于点 , 是直线 上的点,且满足 ,过点 作 轴的平行线交此双曲线于点 .如果 的面积为8,则 的值是 .16. 实验室里有一个水平放置的长方体容器,从内部量得它的高是15cm,底面的长是30cm,宽是20cm,容器内的水深为xcm,现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过定点A的三条棱长分别是10cm,10cm,ycm(y≤15),当铁块的顶部高出水面2cm时,x,y满足的关系式是。
14. 等腰三角形 中,顶角 为 ,点 在以 为圆心, 长为半径的圆上,且 ,则 的度数为 .15. 过双曲线 的动点 作 轴于点 , 是直线 上的点,且满足 ,过点 作 轴的平行线交此双曲线于点 .如果 的面积为8,则 的值是 .16. 实验室里有一个水平放置的长方体容器,从内部量得它的高是15cm,底面的长是30cm,宽是20cm,容器内的水深为xcm,现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过定点A的三条棱长分别是10cm,10cm,ycm(y≤15),当铁块的顶部高出水面2cm时,x,y满足的关系式是。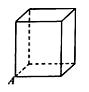
三、解答题
-
17.
(1)、计算: .(2)、解方程: .18. 为了解某地区机动机拥有量对道路通行的影响,学校九年级社会实践小组对2010年~2017年机动车拥有量、车辆经过人民路路口和学校门口的堵车次数进行调查统计,并绘制成下列统计图: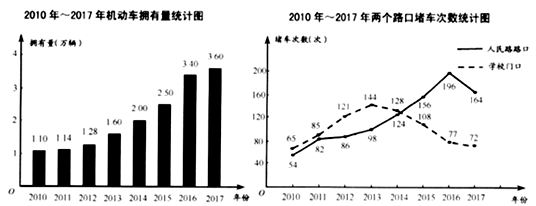
根据统计图,回答下列问题:
(1)、写出2016年机动车的拥有量,分别计算2010年~2017年在人民路路口和学校门口堵车次数的平均数.(2)、根据统计数据,结合生活实际,对机动车拥有量与人民路路口和学校门口堵车次数,说说你的看法.19. 一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量 (升)关于加满油后已行驶的路程 (千米)的函数图象.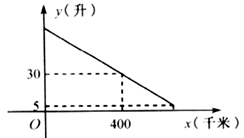 (1)、根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;(2)、求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.20. 学校拓展小组研制了绘图智能机器人(如图1),顺次输入点 , , 的坐标,机器人能根据图2,绘制图形.若图形是线段,求出线段的长度;若图形是抛物线,求出抛物线的解析式.请根据以下点的坐标,求出线段的长度或抛物线的函数关系式.
(1)、根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;(2)、求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.20. 学校拓展小组研制了绘图智能机器人(如图1),顺次输入点 , , 的坐标,机器人能根据图2,绘制图形.若图形是线段,求出线段的长度;若图形是抛物线,求出抛物线的解析式.请根据以下点的坐标,求出线段的长度或抛物线的函数关系式. (1)、 , , ;(2)、 , , .21. 如图1,窗框和窗扇用“滑块铰链”连接.图3是图2中“滑块铰链”的平面示意图,滑轨 安装在窗框上,托悬臂 安装在窗扇上,交点 处装有滑块,滑块可以左右滑动,支点 , , 始终在一直线上,延长 交 于点 .已知 , , .
(1)、 , , ;(2)、 , , .21. 如图1,窗框和窗扇用“滑块铰链”连接.图3是图2中“滑块铰链”的平面示意图,滑轨 安装在窗框上,托悬臂 安装在窗扇上,交点 处装有滑块,滑块可以左右滑动,支点 , , 始终在一直线上,延长 交 于点 .已知 , , .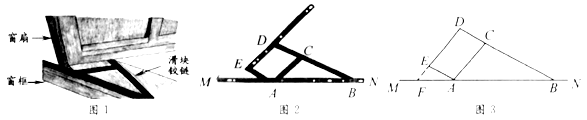 (1)、窗扇完全打开,张角 ,求此时窗扇与窗框的夹角 的度数.(2)、窗扇部分打开,张角 ,求此时点 , 之间的距离(精确到 ).
(1)、窗扇完全打开,张角 ,求此时窗扇与窗框的夹角 的度数.(2)、窗扇部分打开,张角 ,求此时点 , 之间的距离(精确到 ).(参考数据: , )
22. 数学课上,张老师举了下面的例题:例1 等腰三角形 中, ,求 的度数.(答案: )
例2 等腰三角形 中, ,求 的度数.(答案: 或 或 )
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形 中, ,求 的度数.
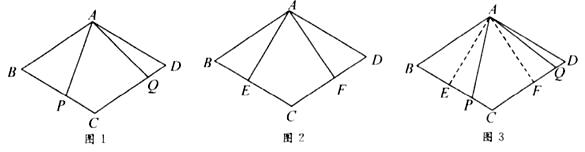
(1)、请你解答以上的变式题.(2)、解(1)后,小敏发现, 的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形 中,设 ,当 有三个不同的度数时,请你探索 的取值范围.23. 小敏思考解决如下问题:原题:如图1,点 , 分别在菱形 的边 , 上, ,求证: .
 (1)、小敏进行探索,若将点 , 的位置特殊化:把 绕点 旋转得到 ,使 ,点 , 分别在边 , 上,如图2,此时她证明了 .请你证明.(2)、受以上(1)的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为 , .请你继续完成原题的证明.(3)、如果在原题中添加条件: , ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).24. 如图,公交车行驶在笔直的公路上,这条路上有 , , , 四个站点,每相邻两站之间的距离为5千米,从 站开往 站的车称为上行车,从 站开往 站的车称为下行车.第一班上行车、下行车分别从 站、 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 , 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
(1)、小敏进行探索,若将点 , 的位置特殊化:把 绕点 旋转得到 ,使 ,点 , 分别在边 , 上,如图2,此时她证明了 .请你证明.(2)、受以上(1)的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为 , .请你继续完成原题的证明.(3)、如果在原题中添加条件: , ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).24. 如图,公交车行驶在笔直的公路上,这条路上有 , , , 四个站点,每相邻两站之间的距离为5千米,从 站开往 站的车称为上行车,从 站开往 站的车称为下行车.第一班上行车、下行车分别从 站、 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 , 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时. (1)、问第一班上行车到 站、第一班下行车到 站分别用时多少?(2)、若第一班上行车行驶时间为 小时,第一班上行车与第一班下行车之间的距离为 千米,求 与 的函数关系式.(3)、一乘客前往 站办事,他在 , 两站间的 处(不含 , 站),刚好遇到上行车, 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到 站或走到 站乘下行车前往 站.若乘客的步行速度是5千米/小时,求 满足的条件.
(1)、问第一班上行车到 站、第一班下行车到 站分别用时多少?(2)、若第一班上行车行驶时间为 小时,第一班上行车与第一班下行车之间的距离为 千米,求 与 的函数关系式.(3)、一乘客前往 站办事,他在 , 两站间的 处(不含 , 站),刚好遇到上行车, 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到 站或走到 站乘下行车前往 站.若乘客的步行速度是5千米/小时,求 满足的条件.