安徽省“皖南八校”2018届高三文数第三次联考试卷
试卷更新日期:2018-06-26 类型:高考模拟
一、单选题
-
1. 已知集合 ,则 ( )
A、 B、 C、 D、2. 已知复数 , 是z的共轭复数,则 =( )
A、 B、 C、1 D、23. 已知等差数列 中, ,前5项和 ,则数列 的公差为( )
A、 B、 C、 D、4. 已知 , , ,则 ( )
A、 B、 C、 D、5. 定义某种运算 的运算原理如右边的流程图所示,则 ( ) A、 B、 C、 D、6. 中国古代数学家名著《九章算术》中记载了一种名为“堑堵”的几何体,其三视图如图所示,则其外接球的表面积为( )
A、 B、 C、 D、6. 中国古代数学家名著《九章算术》中记载了一种名为“堑堵”的几何体,其三视图如图所示,则其外接球的表面积为( ) A、 B、 C、 D、7. 设 满足约束条件 ,则 的最大值为( )
A、 B、 C、 D、7. 设 满足约束条件 ,则 的最大值为( )
A、 B、 C、 D、8. 将函数 的图象上所有点的横坐标缩短到原来的 (纵坐标不变)再把图像向左平移 个单位,得到函数 的图象,则函数 图象的一个对称中心为( )
A、 B、 C、 D、9. 2018年行平昌冬季奥运会与2月9~2月25日举行,为了解奥运会五环所占面积与单独五个环面积和的比例P,某学生设计了如下的计算机模拟,通过计算机模拟项长为8,宽为5的长方形内随机取了N个点,经统计落入五环及其内部的点数为 个,圆环半径为1,则比值 的近似值为( )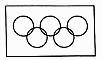 A、 B、 C、 D、10. 函数 的部分图象大致为( )
A、 B、 C、 D、10. 函数 的部分图象大致为( )
A、 B、
B、 C、
C、 D、
D、 11. 已知 分别是双曲线 的左右焦点,过 的直线 与双曲线左右两支分别交于 两点,若 是等边三角形,则该双曲线的离心率为( )
11. 已知 分别是双曲线 的左右焦点,过 的直线 与双曲线左右两支分别交于 两点,若 是等边三角形,则该双曲线的离心率为( )
A、 B、 C、 D、12. 已知 ,若 在区间(0,1)上有且只有一个极值点,则 的取值范围为( )
A、 B、 C、 D、二、填空题
-
13. 已知向量 与 夹角为 ,则 .
14. 若过点 有两条直线与圆 相切,则实数 的取值范围是 .
15. 如图1所示是一种生活中常见的容器,其结构如图2,其中 是矩形, 和 都是等腰梯形,且 平面 ,现测得 , 与 间的距离为 ,则几何体 的体积为 . 16. 已知数列的前 的前 项和为 ,数列的 的前 项和为 ,则满足 的最小 的值为 .
16. 已知数列的前 的前 项和为 ,数列的 的前 项和为 ,则满足 的最小 的值为 .
三、解答题
-
17. 在 中,角 的对边分别为 。
(1)、求角 的大小;(2)、若 ,求 的面积。
18. 如图,已知四棱锥 的底面 是菱形, 平面 ,点 为 的中点。 (1)、求证:平面 平面 ;(2)、求三棱锥 的体积。19. 2017年,在青岛海水稻研究发展宗鑫的试验基地,我国奇数团队培养处的最新一批海水稻活动丰收,由原亩产300公斤,条到最高620公斤,弦长测得其海水盐分浓度月为 。
(1)、求证:平面 平面 ;(2)、求三棱锥 的体积。19. 2017年,在青岛海水稻研究发展宗鑫的试验基地,我国奇数团队培养处的最新一批海水稻活动丰收,由原亩产300公斤,条到最高620公斤,弦长测得其海水盐分浓度月为 。
(1)、对 四种品种水稻随机抽取部分数据,获得如下频率分布直方图,根据直方图,说明这四种品种水稻中,哪一种平均产量最高,哪一种稳定(给出判断即可,不必说明理由); (2)、对盐碱度与抗病害的情况差得如右图和 的列联表的部分数据,填写列表,并以此说明是否有 的把握说明盐碱度对抗病虫害有影响。
(2)、对盐碱度与抗病害的情况差得如右图和 的列联表的部分数据,填写列表,并以此说明是否有 的把握说明盐碱度对抗病虫害有影响。

附表及公式:
 20. 设椭圆 的离心率为 ,椭圆 上一点 到左右两个焦点 的距离之和是4.(1)、求椭圆的方程;(2)、已知过 的直线与椭圆 交于 两点,且两点与左右顶点不重合,若 ,求四边形 面积的最大值。
20. 设椭圆 的离心率为 ,椭圆 上一点 到左右两个焦点 的距离之和是4.(1)、求椭圆的方程;(2)、已知过 的直线与椭圆 交于 两点,且两点与左右顶点不重合,若 ,求四边形 面积的最大值。