江苏省盐城市2018年中考数学试卷
试卷更新日期:2018-06-25 类型:中考真卷
一、选择题
-
1. -2018的相反数是( )A、2018 B、-2018 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、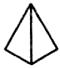 C、
C、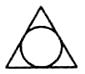 D、
D、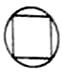 3. 下列运算正确的是( )A、 B、 C、 D、4. 盐通铁路沿线水网密布,河渠纵横,将建设特大桥梁6座,桥梁的总长度约为146000米,将数据146000用科学记数法表示为( )A、 B、 C、 D、5. 如图是由5个大小相同的小正方体组成的几何体,则它的左视图是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 盐通铁路沿线水网密布,河渠纵横,将建设特大桥梁6座,桥梁的总长度约为146000米,将数据146000用科学记数法表示为( )A、 B、 C、 D、5. 如图是由5个大小相同的小正方体组成的几何体,则它的左视图是( ) A、
A、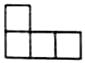 B、
B、 C、
C、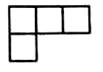 D、
D、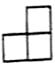 6. 一组数据2,4,6,4,8的中位数为( )A、2 B、4 C、6 D、87. 如图, 为 的直径, 是 的弦, ,则 的度数为( )
6. 一组数据2,4,6,4,8的中位数为( )A、2 B、4 C、6 D、87. 如图, 为 的直径, 是 的弦, ,则 的度数为( )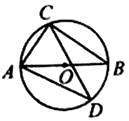 A、 B、 C、 D、8. 已知一元二次方程 有一个根为1,则 的值为( )A、-2 B、2 C、-4 D、4
A、 B、 C、 D、8. 已知一元二次方程 有一个根为1,则 的值为( )A、-2 B、2 C、-4 D、4二、填空题
-
9. 根据如图所示的车票信息,车票的价格为元.
 10. 要使分式 有意义,则 的取值范围是 .11. 分解因式: .12. 一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为 .
10. 要使分式 有意义,则 的取值范围是 .11. 分解因式: .12. 一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为 . 13. 将一个含有 角的直角三角板摆放在矩形上,如图所示,若 ,则 .
13. 将一个含有 角的直角三角板摆放在矩形上,如图所示,若 ,则 .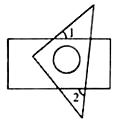 14. 如图,点 为矩形 的 边的中点,反比例函数 的图象经过点 ,交 边于点 .若 的面积为1,则 。
14. 如图,点 为矩形 的 边的中点,反比例函数 的图象经过点 ,交 边于点 .若 的面积为1,则 。 15. 如图,左图是由若干个相同的图形(右图)组成的美丽图案的一部分.右图中,图形的相关数据:半径 , .则右图的周长为 (结果保留 ).
15. 如图,左图是由若干个相同的图形(右图)组成的美丽图案的一部分.右图中,图形的相关数据:半径 , .则右图的周长为 (结果保留 ).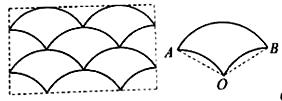 16. 如图,在直角 中, , , , 、 分别为边 、 上的两个动点,若要使 是等腰三角形且 是直角三角形,则 .
16. 如图,在直角 中, , , , 、 分别为边 、 上的两个动点,若要使 是等腰三角形且 是直角三角形,则 .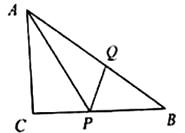
三、解答题
-
17. 计算: .18. 解不等式: ,并把它的解集在数轴上表示出来.
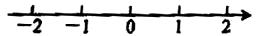 19. 先化简、再求值: ,其中 .20. 端午节是我国传统佳节.小峰同学带了4个粽子(除粽馅不同外,其它均相同),其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子,准备从中任意拿出两个送给他的好朋友小悦.(1)、用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果;(2)、请你计算小悦拿到的两个粽子都是肉馅的概率.21. 在正方形 中,对角线 所在的直线上有两点 、 满足 ,连接 、 、 、 ,如图所示.
19. 先化简、再求值: ,其中 .20. 端午节是我国传统佳节.小峰同学带了4个粽子(除粽馅不同外,其它均相同),其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子,准备从中任意拿出两个送给他的好朋友小悦.(1)、用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果;(2)、请你计算小悦拿到的两个粽子都是肉馅的概率.21. 在正方形 中,对角线 所在的直线上有两点 、 满足 ,连接 、 、 、 ,如图所示.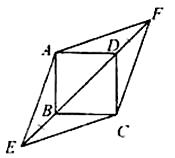 (1)、求证: ;(2)、试判断四边形 的形状,并说明理由.22. “安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:
(1)、求证: ;(2)、试判断四边形 的形状,并说明理由.22. “安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:.仅学生自己参与; .家长和学生一起参与;
.仅家长自己参与; .家长和学生都未参与.
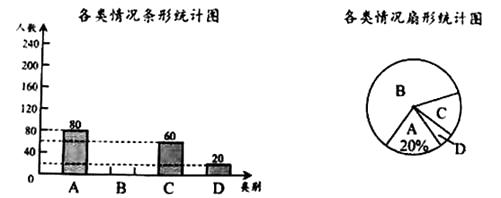
请根据图中提供的信息,解答下列问题:
(1)、在这次抽样调查中,共调查了名学生;(2)、补全条形统计图,并在扇形统计图中计算 类所对应扇形的圆心角的度数;(3)、根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.23. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价3元,则平均每天销售数量为件;(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?24. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离 (米)与时间 (分钟)之间的函数关系如图所示. (1)、根据图象信息,当 分钟时甲乙两人相遇,甲的速度为米/分钟;(2)、求出线段 所表示的函数表达式.25. 如图,在以线段 为直径的 上取一点,连接 、 .将 沿 翻折后得到 .
(1)、根据图象信息,当 分钟时甲乙两人相遇,甲的速度为米/分钟;(2)、求出线段 所表示的函数表达式.25. 如图,在以线段 为直径的 上取一点,连接 、 .将 沿 翻折后得到 .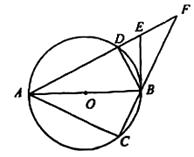 (1)、试说明点 在 上;
(1)、试说明点 在 上;
(2)、在线段 的延长线上取一点 ,使 .求证: 为 的切线;
(3)、在(2)的条件下,分别延长线段 、 相交于点 ,若 , ,求线段 的长.
26.(1)、【发现】如图①,已知等边 ,将直角三角形的 角顶点 任意放在 边上(点 不与点 、 重合),使两边分别交线段 、 于点 、 .
①若 , , ,则 ;
②求证: .
(2)、【思考】若将图①中的三角板的顶点 在 边上移动,保持三角板与 、 的两个交点 、 都存在,连接 ,如图②所示.问点 是否存在某一位置,使 平分 且 平分 ?若存在,求出 的值;若不存在,请说明理由.(3)、【探索】如图③,在等腰 中, ,点 为 边的中点,将三角形透明纸板的一个顶点放在点 处(其中 ),使两条边分别交边 、 于点 、 (点 、 均不与 的顶点重合),连接 .设 ,则 与 的周长之比为(用含 的表达式表示).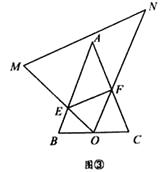 27. 如图①,在平面直角坐标系 中,抛物线 经过点 、 两点,且与 轴交于点 .
27. 如图①,在平面直角坐标系 中,抛物线 经过点 、 两点,且与 轴交于点 .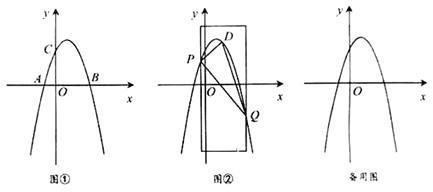 (1)、求抛物线的表达式;(2)、如图②,用宽为4个单位长度的直尺垂直于 轴,并沿 轴左右平移,直尺的左右两边所在的直线与抛物线相交于 、 两点(点 在点 的左侧),连接 ,在线段 上方抛物线上有一动点 ,连接 、 .
(1)、求抛物线的表达式;(2)、如图②,用宽为4个单位长度的直尺垂直于 轴,并沿 轴左右平移,直尺的左右两边所在的直线与抛物线相交于 、 两点(点 在点 的左侧),连接 ,在线段 上方抛物线上有一动点 ,连接 、 .(Ⅰ)若点 的横坐标为 ,求 面积的最大值,并求此时点 的坐标;
(Ⅱ)直尺在平移过程中, 面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.