江苏省兴化市顾庄学区三校2016-2017学年七年级下学期数学期末考试试卷
试卷更新日期:2018-06-25 类型:期末考试
一、单选题
-
1. 化简﹣b•b3•b4的正确结果是( )A、﹣b7 B、b7 C、-b8 D、b82. 已知 是关于x、y的方程4kx-3y=-1的一个解,则k的值为( )A、1 B、-1 C、2 D、-23. 不等式2x+1≥5的解集在数轴上表示正确的是 ( )A、
 B、
B、 C、
C、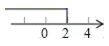 D、
D、 4. 若多项式 = ,则a,b的值分别是( )A、 , B、 , C、 , D、 ,5. 下列命题中,为真命题的是( )A、如果-2x>-2,那么x>1 B、如果a2=b2 , 那么a3=b3 C、面积相等的三角形全等 D、如果a∥b,b∥c,那么a∥c6.
4. 若多项式 = ,则a,b的值分别是( )A、 , B、 , C、 , D、 ,5. 下列命题中,为真命题的是( )A、如果-2x>-2,那么x>1 B、如果a2=b2 , 那么a3=b3 C、面积相等的三角形全等 D、如果a∥b,b∥c,那么a∥c6.如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
7. 生物学家发现了一种病毒的长度约为0.00000432毫米,数据0.00000432用科学记数法表示为 .8. 一个长方体的长、宽、高分别是3x-4,2x和x,它的体积等于
9. 不等式组 的解集是 .10. 命题“如果a>b,那么ac>bc ” 的逆命题是命题(填“真”或“假”).
11. 如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件 , 使△ABC≌△DBE(只需添加一个即可,不添加辅助线). 12. 已知a+b=3,ab=2,则(a-b)2= .13. 如图,已知∠1=∠2=90°,AD=AE,那么图中有对全等三角形.
12. 已知a+b=3,ab=2,则(a-b)2= .13. 如图,已知∠1=∠2=90°,AD=AE,那么图中有对全等三角形. 14. 某地准备对一段长120 m的河道进行清淤疏通.若甲工程队先用 4天单独完成其中一部分河道的疏通任务,则余下的任务由乙工程队单独完成需要9天;若甲工程队先单独工作8天,则余下的任务由乙工程队单独完成需要3天.设甲工程队平均每天疏通河道xm,乙工程队平均每天疏通河道y m,则 的值为 .
14. 某地准备对一段长120 m的河道进行清淤疏通.若甲工程队先用 4天单独完成其中一部分河道的疏通任务,则余下的任务由乙工程队单独完成需要9天;若甲工程队先单独工作8天,则余下的任务由乙工程队单独完成需要3天.设甲工程队平均每天疏通河道xm,乙工程队平均每天疏通河道y m,则 的值为 .
15. 已知关于 的不等式组 的整数解共有3个,则 的取值范围是 .16. 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出了(a+b)n(n=1,2,3,4,……)的展开式的系数规律(按n的次数由大到小的顺序):
请依据上述规律,写出(x-2)2017展开式中含x2016项的系数是 .
三、解答题
-
17. 计算:
(1)、(2)、已知x2+x﹣5=0,求代数式(x﹣1)2﹣x(x﹣3)+(x+2)(x﹣2)的值.18. 因式分解:
(1)、2x3y-8xy;(2)、 .19. 解不等式 ,把它的解集在数轴上表示出来,并求出这个不等式的负整数解. 20. 如图,点D在AB上,点E在AC上,BE、CD相交于点O.
20. 如图,点D在AB上,点E在AC上,BE、CD相交于点O. (1)、若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(1)、若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)、试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.21. 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,问A型节能灯最多可以买多少只?
22. 如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证: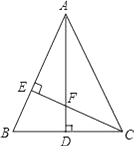 (1)、△AEF≌△CEB;(2)、AF=2CD.23. 已知关于x、y的方程组(1)、求方程组的解(用含m的代数式表示);(2)、若方程组的解满足条件x<0,且y<0,求m的取值范围.
(1)、△AEF≌△CEB;(2)、AF=2CD.23. 已知关于x、y的方程组(1)、求方程组的解(用含m的代数式表示);(2)、若方程组的解满足条件x<0,且y<0,求m的取值范围.
24. 如图,直线m与直线n互相垂直,垂足为O , A、B两点同时从点O出发,点A沿直线m向左运动,点B沿直线n向上运动. (1)、若∠BAO和∠ABO的平分线相交于点P , 在点A、B的运动过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;(2)、若△ABO的两个外角的平分线AQ、BQ相交于点Q , AP的延长线交QB的延长线于点C,在点A、B的运动过程中,∠Q和∠C的大小是否会发生变化?若不发生变 化,请求出∠Q和∠C的度数;若发生变化,请说明理由.
(1)、若∠BAO和∠ABO的平分线相交于点P , 在点A、B的运动过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;(2)、若△ABO的两个外角的平分线AQ、BQ相交于点Q , AP的延长线交QB的延长线于点C,在点A、B的运动过程中,∠Q和∠C的大小是否会发生变化?若不发生变 化,请求出∠Q和∠C的度数;若发生变化,请说明理由.
25. 观察下列关于自然数的等式:a1:32-12=8×1;
a2:52-32=8×2;
a3:72-52=8×3;……
根据上述规律解决下列问题:
(1)、写出第a4个等式:;
(2)、写出你猜想的第an个等式(用含n的式子表示),并验证其正确性;(3)、对于正整数k,若ak , ak+1 , ak+2为△ABC的三边,求k的取值范围.26. 已知A=2 a -7,B=a2- 4a+3,C= a2 +6a-28,其中 .
(1)、求证:B-A>0,并指出A与B的大小关系;
(2)、阅读对B因式分解的方法:解:B=a2- 4a+3=a2- 4a+4-1=(a-2)2-1=(a-2+1)(a-2-1)=(a-1)(a-3).
请完成下面的两个问题:
①仿照上述方法分解因式:x2- 4x-96;
②指出A与C哪个大?并说明你的理由.