浙江省杭州市2018年中考数学试题
试卷更新日期:2018-06-23 类型:中考真卷
一、选择题
-
1. =( )A、3 B、-3 C、 D、2. 数据1800000用科学记数法表示为( )A、1.86 B、1.8×106 C、18×105 D、18×1063. 下列计算正确的是( )A、 B、 C、 D、4. 测试五位学生“一分钟跳绳”成绩,得到五个各不相同的数据,统计时,出现了一处错误:将最高成绩写得更高了。计算结果不受影响的是( )
A、方差 B、标准差 C、中位数 D、平均数5. 若线段AM,AN分别是△ABC边上的高线和中线,则( )
A、 B、 C、 D、6. 某次知识竞赛共有20道题,规定:每答对一题得+5分,每答错一题得-2分,不答的题得0分。已知圆圆这次竞赛得了60分,设圆圆答对了 道题,答错了 道题,则( )
A、 B、 C、 D、7. 一个两位数,它的十位数字是3,个位数字是抛掷一枚质地均匀的骰子(六个面分别有数字1—6)朝上一面的数字。任意抛掷这枚骰子一次,得到的两位数是3的倍数的概率等于( )
A、 B、 C、 D、8. 如图,已知点P矩形ABCD内一点(不含边界),设 , , , ,若 , ,则( ) A、 B、 C、 D、9. 四位同学在研究函数 (b,c是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, .已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A、 B、 C、 D、9. 四位同学在研究函数 (b,c是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, .已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A、甲 B、乙 C、丙 D、丁10. 如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1 , S2 , ( )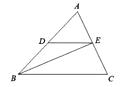 A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则
A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则二、填空题
-
11. 计算:a-3a=。12. 如图,直线a∥b,直线c与直线a,b分别交于A,B,若∠1=45°,则∠2=。
 13. 因式分解:14. 如图,AB是⊙的直径,点C是半径OA的中点,过点C作DE⊥AB,交O于点D,E两点,过点D作直径DF,连结AF,则∠DEA=。
13. 因式分解:14. 如图,AB是⊙的直径,点C是半径OA的中点,过点C作DE⊥AB,交O于点D,E两点,过点D作直径DF,连结AF,则∠DEA=。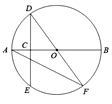 15. 某日上午,甲、乙两车先后从A地出发沿一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度v(单位:千米/小时)的范围是。
15. 某日上午,甲、乙两车先后从A地出发沿一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度v(单位:千米/小时)的范围是。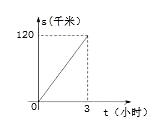 16. 折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=。
16. 折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=。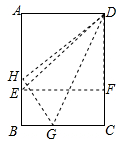
三、简答题
-
17. 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货,设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)。(1)、求v关于t的函数表达式(2)、若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?18. 某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数和频数直方图(每组含前一个边界值,不含后一个边界值)。

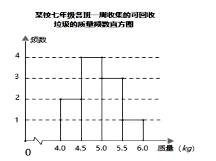 (1)、求a的值。(2)、已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元。19. 如图,在△ABC中,AB=AC,AD为BC边上的中线DE⊥AB于点E。
(1)、求a的值。(2)、已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元。19. 如图,在△ABC中,AB=AC,AD为BC边上的中线DE⊥AB于点E。 (1)、求证:△BDE∽△CAD。(2)、若AB=13,BC=10,求线段DE的长20. 设一次函数 ( 是常数, )的图象过A(1,3),B(-1,-1)
(1)、求证:△BDE∽△CAD。(2)、若AB=13,BC=10,求线段DE的长20. 设一次函数 ( 是常数, )的图象过A(1,3),B(-1,-1)
(1)、求该一次函数的表达式;(2)、若点(2a+2,a2)在该一次函数图象上,求a的值;(3)、已知点C(x1 , y1),D(x2 , y2)在该一次函数图象上,设m=(x1-x2)(y1-y2),判断反比例函数 的图象所在的象限,说明理由。21. 如图,在△ABC中,∠ACB=90°,以点B为圆心,BC的长为半径画弧,交线段AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD。 (1)、若∠A=28°,求∠ACD的度数;(2)、设BC=a,AC=b;
(1)、若∠A=28°,求∠ACD的度数;(2)、设BC=a,AC=b;①线段AD的长度是方程 的一个根吗?说明理由。
②若线段AD=EC,求 的值.
22. 设二次函数 (a,b是常数,a≠0)(1)、判断该二次函数图象与x轴交点的个数,说明理由.(2)、若该二次函数的图象经过A(-1,4),B(0,-1),C(1,1)三个点中的其中两个点,求该二次函数的表达式;(3)、若a+b<0,点P(2,m)(m>0)在该二次函数图象上,求证:a>0.23. 如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设 。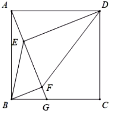 (1)、求证:AE=BF;(2)、连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)、设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2 , 求 的最大值.
(1)、求证:AE=BF;(2)、连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)、设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2 , 求 的最大值.