四川省成都市2018年中考数学试卷
试卷更新日期:2018-06-23 类型:中考真卷
一、选择题(A卷)
-
1. 实数 在数轴上对应的点的位置如图所示,这四个数中最大的是( )
 A、 B、 C、 D、2. 2018年5月21日,西昌卫星发射中心成功发射探月工程嫦娥四号任务“鹊桥号”中继星,卫星进入近地点高度为200公里、远地点高度为40万公里的预定轨道.将数据40万用科学记数法表示为( )
A、 B、 C、 D、2. 2018年5月21日,西昌卫星发射中心成功发射探月工程嫦娥四号任务“鹊桥号”中继星,卫星进入近地点高度为200公里、远地点高度为40万公里的预定轨道.将数据40万用科学记数法表示为( )
A、 B、 C、 D、3. 如图所示的正六棱柱的主视图是( )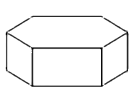 A、
A、 B、
B、 C、
C、 D、
D、 4. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、 B、 C、 D、5. 下列计算正确的是( )A、x2+x2=x4 B、(x-y)2=x2-y2 C、(x2y)3=x6y D、(-x)2·x3=x56. 如图,已知 ,添加以下条件,不能判定 的是( )
4. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、 B、 C、 D、5. 下列计算正确的是( )A、x2+x2=x4 B、(x-y)2=x2-y2 C、(x2y)3=x6y D、(-x)2·x3=x56. 如图,已知 ,添加以下条件,不能判定 的是( )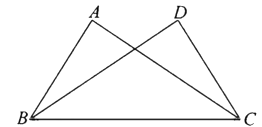 A、 B、 C、 D、7. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )
A、 B、 C、 D、7. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )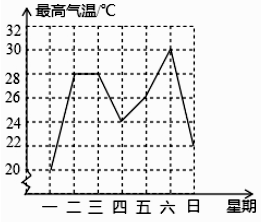 A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃8. 分式方程 的解是( )A、x=1 B、 C、x=3 D、9. 如图,在 中, , 的半径为3,则图中阴影部分的面积是( )
A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃8. 分式方程 的解是( )A、x=1 B、 C、x=3 D、9. 如图,在 中, , 的半径为3,则图中阴影部分的面积是( )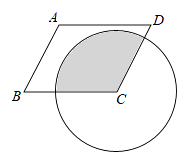 A、 B、 C、 D、10. 关于二次函数 ,下列说法正确的是( )A、图像与 轴的交点坐标为 B、图像的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-3
A、 B、 C、 D、10. 关于二次函数 ,下列说法正确的是( )A、图像与 轴的交点坐标为 B、图像的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-3二、填空题(A卷)
-
11. 等腰三角形的一个底角为 ,则它的顶角的度数为 .
12. 在一个不透明的盒子中,装有除颜色外完全相同的乒乓球共16个,从中随机摸出一个乒乓球,若摸到黄色乒乓球的概率为 ,则该盒子中装有黄色兵乓球的个数是 .
13. 已知 ,且 ,则 的值为 .14. 如图,在矩形 中,按以下步骤作图:①分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ;②作直线 交 于点 .若 , ,则矩形的对角线 的长为 .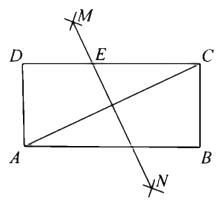
三、解答题(A卷)
-
15.
(1)、 .(2)、化简 .16. 若关于 的一元二次方程 有两个不相等的实数根,求 的取值范围.
17. 为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.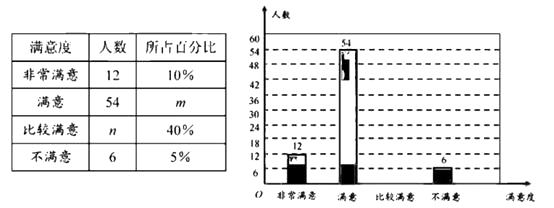
根据图标信息,解答下列问题:
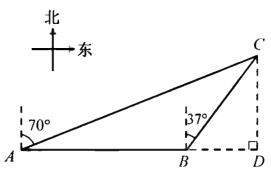
(1)、本次调查的总人数为 , 表中 的值;(2)、请补全条形统计图;(3)、据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.18. 由我国完全自主设计、自主建造的首舰国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛 位于它的北偏东 方向,且于航母相距80海里,再航行一段时间后到达处,测得小岛 位于它的北偏东 方向.如果航母继续航行至小岛 的正南方向的 处,求还需航行的距离 的长.(参考数据: , , , , , )
 19. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .
19. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .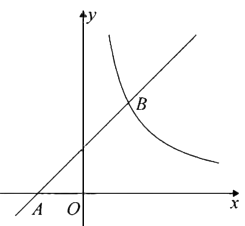 (1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
(1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
20. 如图,在 中, , 平分 交 于点 , 为 上一点,经过点 , 的 分别交 , 于点 , ,连接 交 于点 .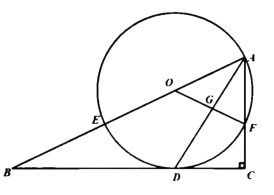 (1)、求证: 是 的切线;(2)、设 , ,试用含 的代数式表示线段 的长;(3)、若 , ,求 的长.
(1)、求证: 是 的切线;(2)、设 , ,试用含 的代数式表示线段 的长;(3)、若 , ,求 的长.四、填空题(B卷)
-
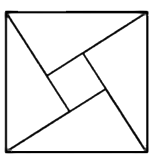
21. 已知 , ,则代数式 的值为.22. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为 ,现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为.
 23. 已知 , , , , , ,…(即当 为大于1的奇数时, ;当 为大于1的偶数时, ),按此规律, .24. 如图,在菱形 中, , 分别在边 上,将四边形 沿 翻折,使 的对应线段 经过顶点 ,当 时, 的值为.
23. 已知 , , , , , ,…(即当 为大于1的奇数时, ;当 为大于1的偶数时, ),按此规律, .24. 如图,在菱形 中, , 分别在边 上,将四边形 沿 翻折,使 的对应线段 经过顶点 ,当 时, 的值为.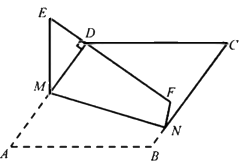 25. 设双曲线 与直线 交于 , 两点(点 在第三象限),将双曲线在第一象限的一支沿射线 的方向平移,使其经过点 ,将双曲线在第三象限的一支沿射线 的方向平移,使其经过点 ,平移后的两条曲线相交于点 , 两点,此时我称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”, 为双曲线的“眸径”当双曲线 的眸径为6时, 的值为.
25. 设双曲线 与直线 交于 , 两点(点 在第三象限),将双曲线在第一象限的一支沿射线 的方向平移,使其经过点 ,将双曲线在第三象限的一支沿射线 的方向平移,使其经过点 ,平移后的两条曲线相交于点 , 两点,此时我称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”, 为双曲线的“眸径”当双曲线 的眸径为6时, 的值为.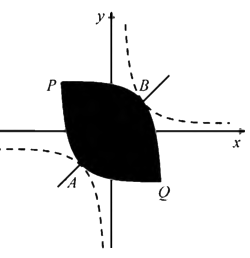
五、解答题 (B卷)
-
26. 为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用 (元)与种植面积 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
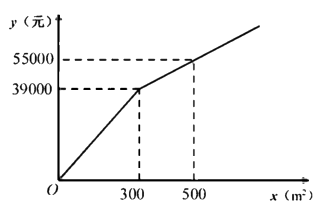 (1)、直接写出当 和 时, 与 的函数关系式;
(1)、直接写出当 和 时, 与 的函数关系式;
(2)、广场上甲、乙两种花卉的种植面积共 ,若甲种花卉的种植面积不少于 ,且不超过乙种花卉种植面积的2倍,那么应该怎忙分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?27. 在 中, , , ,过点 作直线 ,将 绕点 顺时针得到 (点 , 的对应点分别为 , )射线 , 分别交直线 于点 , .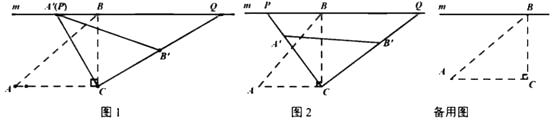 (1)、如图1,当 与 重合时,求 的度数;(2)、如图2,设 与 的交点为 ,当 为 的中点时,求线段 的长;
(1)、如图1,当 与 重合时,求 的度数;(2)、如图2,设 与 的交点为 ,当 为 的中点时,求线段 的长;
(3)、在旋转过程时,当点 分别在 , 的延长线上时,试探究四边形 的面积是否存在最小值.若存在,求出四边形 的最小面积;若不存在,请说明理由.28. 如图,在平面直角坐标系 中,以直线 为对称轴的抛物线 与直线 交于 , 两点,与 轴交于 ,直线 与 轴交于 点.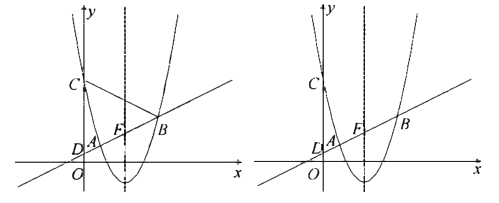 (1)、求抛物线的函数表达式;(2)、设直线 与抛物线的对称轴的交点为 、 是抛物线上位于对称轴右侧的一点,若 ,且 与 面积相等,求点 的坐标;(3)、若在 轴上有且仅有一点 ,使 ,求 的值.
(1)、求抛物线的函数表达式;(2)、设直线 与抛物线的对称轴的交点为 、 是抛物线上位于对称轴右侧的一点,若 ,且 与 面积相等,求点 的坐标;(3)、若在 轴上有且仅有一点 ,使 ,求 的值.