浙江省台州市温岭五校联考2016-2017学年上学期八年级期末考试数学试卷

试卷更新日期：2017-01-13 类型：期末考试

进入出卷网下载

一、选择題（共10小题，每小题3分，共30分）

1. 下列图形中，轴对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（）

A、8cm，4cm，3cm B、3cm，6cm，9cm C、9cm，12cm，13cm D、13cm，11cm，2cm

查看试题解析
3. 花粉的质量很小，一粒某种植物花粉的质量约为0.000037毫克，那么数0.000037可用科学记数法表示为（）

A、3.7×10^﹣5 B、3.7×10^﹣6 C、37×10^﹣7 D、3.7×10^﹣8

查看试题解析
4. 下列各式中，计算正确的是（）

A、x（2x-1）=2x²-1 B、 $\frac{x + 3}{x^{2} - 9} = \frac{1}{x - 3}$ C、（a+2）²=a²+4 D、（x+2）（x-3）=x²+x-6

查看试题解析
5.
如图，△ABC 和 △DCE中， AB＝DC，BC＝CE，∠A＝55°，∠ACB=80°，∠DCE=45°，则∠D的度数是（）

A、45° B、55° C、80° D、100°

查看试题解析
6.
工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与点M，N重合，过角尺顶点C作射线OC，则OC平分∠AOB．由此作法可得△MOC≌△NOC，其依据是（）

A、SSS B、SAS C、ASA D、AAS

查看试题解析
7. 从正面看圆锥，看到的是一个等腰三角形。已知这个等腰三角形的两边长分别是3和7，则从正面看圆锥得到的图形的周长为（）

A、13或17 B、13 C、15 D、17

查看试题解析
8. 小方是一位密码编译爱好者，在他的密码手册中，有这样一条信息： $a - b ， x - y ，$ $x + y ， a + b ， x^{2} - y^{2} ， a^{2} - b^{2}$ ,分别对应下列六个字：州，爱，我，台，赞，美.现将 $（ x^{2} - y^{2} ） a^{2} - （ x^{2} - y^{2} ） b^{2}$ 因式分解，结果呈现的密码信息可能是（）

A、赞美 B、台州赞 C、爱我台州 D、我爱美

查看试题解析
9. 为加快“最美台州”环境建设，某园林公司增加了人力进行大型树木移植，现在平均每天比原计划多植树30棵，现在植树400棵所需时间与原计划植树300棵所需时间相同，设现在平均每天植树x棵，则列出的方程为（）

A、 $\frac{400}{x} = \frac{300}{x + 30}$ B、 $\frac{400}{x - 30} = \frac{300}{x}$ C、 $\frac{400}{x + 30} = \frac{300}{x}$ D、 $\frac{400}{x} = \frac{300}{x - 30}$

查看试题解析
10.
如图，在第1个△A₁BC中，∠B=30°，A₁B=CB；在边A₁B上任取一点D，延长CA₁到A₂ ，使A₁A₂=A₁D，得到第2个△A₁A₂D；在边A₂D上任取一点E，延长A₁A₂到A₃ ，使A₂A₃=A₂E，得到第3个△A₂A₃E，…按此做法继续下去，则第(n+1)个三角形以 $A_{n}$ 为顶点的内角的度数是（）

A、 ${(\frac{1}{2})}^{n- 1} \times 75 °$ B、 ${(\frac{1}{2})}^{n} \times 75 °$ C、 $180 ° - {(\frac{1}{2})}^{n- 1} \times 75 °$ D、 $180 ° - {(\frac{1}{2})}^{n} \times 75 °$

查看试题解析

二、填空題（共10小题，每小題3分，共30分）

11. 分解因式：m²﹣16= ．

查看试题解析
12. 点（﹣2，﹣5）关于y轴对称的点的坐标是．

查看试题解析
13. 分式 $\frac{2 x -4}{x + 3}$ 的值为0，则x的值为.

查看试题解析
14. 我们知道三角形的内角和是180°，四边形的内角和可以转化成两个三角形的内角和来得到是360°，那十二边形的内角和是°．

查看试题解析
15.
如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P₁ ， P₂ ， P₃ ， P₄四个点中找出符合条件的点P，则点P有个.

查看试题解析
16.
如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式　．

查看试题解析
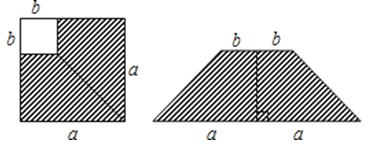17.
如图：△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，则△ABC的周长为cm．

查看试题解析
18. 等腰三角形一腰上的高与另一腰的夹角为36°，则该等腰三角形的底角的度数为.

查看试题解析
19.
如图所示，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；
③△ACN≌△ABM；④CD=DN．其中正确的是（将正确的结论的序号都填上）．

查看试题解析
20.
如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=2，则EF= ．

查看试题解析

三、综合题

21. 计算题：

(1)、 $728^{2} - 272^{2}$

(2)、因式分解： ${(a - 2)}^{2} - 3 (2 - a)$

(3)、解方程： $\frac{2}{x + 3} = \frac{1}{x - 1}$

查看试题解析
22. 平面直角坐标系中，△ABC与△PQR关于x轴对称，已知点P(-4，-1)，Q(-2，4)，R(1，1)，点A与点P对称，点B与点Q对称。

(1)、
在图中作出△ABC，并指出点A，B，C的坐标；

(2)、若△PQR内有一点是（m，1），则△ABC内与它对称的点坐标是；

(3)、△ABC的面积是.

查看试题解析
23.
如图，在△ABC中，AB＝AC，AD⊥BC，CE⊥AB，AE＝CE．求证：

(1)、△AEF≌△CEB；

(2)、AF＝2CD．

查看试题解析
24. 请在下列两题中选取一题解答：

(1)、已知a是方程 $\frac{2}{a + 1} = 1$ 的解，求代数式（a﹣1）²﹣a（a﹣3）的值；

(2)、化简： $\frac{x^{2} + 4 x + 4}{x^{2} + 2 x} \div (2 x - \frac{4 + x^{2}}{x})$ ，在不等式x≤2的非负整数解中选择一个适当的数代入求值．

查看试题解析
25. 早晨，小金步行到离家900米的学校去上学，到学校时发现眼镜忘在家中，于是他立即按原路步行回家，拿到眼镜后立即按原路骑自行车返回学校．已知小金步行从学校到家所用的时间比骑自行车从家到学校所用的时间多10分钟，已知小金骑自行车速度是步行速度的3倍．

(1)、求小金步行速度和自行车速度各是多少？（单位：米/分）

(2)、下午放学后，小金骑自行车回到家，然后步行去图书馆，如果小金骑自行车和步行的速度不变，小金步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍，那么小金家与图书馆之间的路程最多是多少米？

查看试题解析
26. 动手操作题：如何能把一个三角形分成两个等腰三角形吗？
实际上，一个三角形只要具备下列三个条件之一，都可以被分成两个等腰三角形：
①一个角为90°；②一个角是另一个的2倍（第三角必须大于45°）；
③一个角是另一个角的3倍.今天，我们通过作图来验证这个结论。

(1)、
问题1：
如图，Rt△ABC中，求画一条直线l将△ABC分成两个等腰三角形.并说明直线l与△ABC
边上的交点D的位置.

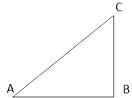
(2)、
问题2：
如图，△ABC中，∠ACB=80°， ∠BAC=40°，求画一条直线l把△ABC分成两个等腰三角形，并在图中标注两个顶角的度数.

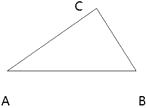
(3)、
问题3：
如图，△ABC中，∠ACB=120°， ∠BAC=40°，求画一条直线l把△ABC分成两个等腰三角形，并在图中标注两个顶角的度数.

(4)、问题：4：
如果等腰三角形能被一条直线分成两个等腰三角形，则原等腰三角形的顶角可以是°.（至少写出三个）

(5)、拓展：已知△ABC的三条边长分别为3，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（）

A、6条 B、7条 C、8条 D、9条

查看试题解析

浙江省台州市温岭五校联考2016-2017学年上学期八年级期末考试数学试卷

一、选择題（共10小题，每小题3分，共30分）

二、 填空題（共10小题，每小題3分，共30分）

三、综合题

二、填空題（共10小题，每小題3分，共30分）