广东省广州市2018年中考数学试题
试卷更新日期:2018-06-21 类型:中考真卷
一、选择题
-
1. 四个数0,1, , 中,无理数的是( )A、 B、1 C、 D、02. 如图所示的五角星是轴对称图形,它的对称轴共有( )
 A、1条 B、3条 C、5条 D、无数条3. 如图所示的几何体是由4个相同的小正方体搭成的,它的主视图是( )
A、1条 B、3条 C、5条 D、无数条3. 如图所示的几何体是由4个相同的小正方体搭成的,它的主视图是( )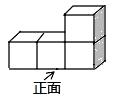 A、
A、 B、
B、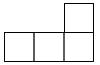 C、
C、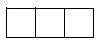 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,直线AD,BC被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,直线AD,BC被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )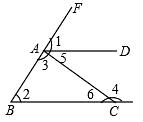 A、∠4,∠2 B、∠2,∠6 C、∠5,∠4 D、∠2,∠46. 甲袋中装有2个相同的小球,分别写有数字1和2,乙袋中装有2个相同的小球,分别写有数字1和2,从两个口袋中各随机取出1个小球,取出的两个小球上都写有数字2的概率是( )A、 B、 C、 D、7. 如图,AB是圆O的弦,OC⊥AB,交圆O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是( )
A、∠4,∠2 B、∠2,∠6 C、∠5,∠4 D、∠2,∠46. 甲袋中装有2个相同的小球,分别写有数字1和2,乙袋中装有2个相同的小球,分别写有数字1和2,从两个口袋中各随机取出1个小球,取出的两个小球上都写有数字2的概率是( )A、 B、 C、 D、7. 如图,AB是圆O的弦,OC⊥AB,交圆O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是( )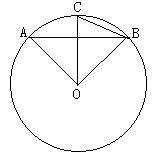 A、40° B、50° C、70° D、80°8. 《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚黄金重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13辆(袋子重量忽略不计),问黄金、白银每枚各重多少两?设每枚黄金重x辆,每枚白银重y辆,根据题意得( )A、 B、 C、 D、9. 一次函数 和反比例函数 在同一直角坐标系中大致图像是( )
A、40° B、50° C、70° D、80°8. 《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚黄金重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13辆(袋子重量忽略不计),问黄金、白银每枚各重多少两?设每枚黄金重x辆,每枚白银重y辆,根据题意得( )A、 B、 C、 D、9. 一次函数 和反比例函数 在同一直角坐标系中大致图像是( )
A、 B、
B、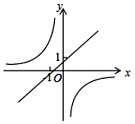 C、
C、 D、
D、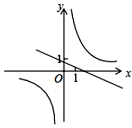 10. 在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到 ,第2次移动到 ……,第n次移动到 ,则△ 的面积是( )
10. 在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到 ,第2次移动到 ……,第n次移动到 ,则△ 的面积是( )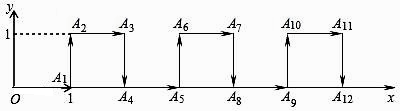 A、504 B、 C、 D、
A、504 B、 C、 D、二、填空题
-
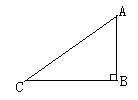
11. 已知二次函数 ,当x>0时,y随x的增大而(填“增大”或“减小”)12. 如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=。
 13. 方程 的解是14. 如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0)点D在y轴上,则点C的坐标是。
13. 方程 的解是14. 如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0)点D在y轴上,则点C的坐标是。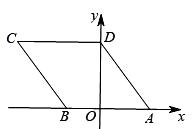 15. 如图,数轴上点A表示的数为a,化简: =
15. 如图,数轴上点A表示的数为a,化简: =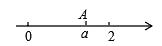 16. 如图9,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:
16. 如图9,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论: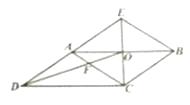
①四边形ACBE是菱形;②∠ACD=∠BAE
③AF:BE=2:3 ④
其中正确的结论有。(填写所有正确结论的序号)
三、解答题
-
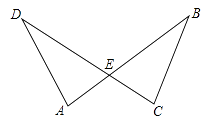
17. 解不等式组18. 如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C。
 19. 已知(1)、化简T。(2)、若正方形ABCD的边长为a,且它的面积为9,求T的值。20. 随着移动互联网的快速发展,基于互联网的共享单车应运而生,为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.(1)、这组数据的中位数是 , 众数是 .(2)、计算这10位居民一周内使用共享单车的平均次数;(3)、若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数。21. 友谊商店A型号笔记本电脑的售价是a元/台,最近,该商店对A型号笔记本电脑举行促销活动,有两种优惠方案,方案一:每台按售价的九折销售,方案二:若购买不超过5台,每台按售价销售,若超过5台,超过的部分每台按售价的八折销售,某公司一次性从友谊商店购买A型号笔记本电脑x台。(1)、当x=8时,应选择哪种方案,该公司购买费用最少?最少费用是多少元?(2)、若该公司采用方案二方案更合算,求x的范围。22. 设P(x,0)是x轴上的一个动点,它与原点的距离为 。(1)、求 关于x的函数解析式,并画出这个函数的图象(2)、若反比例函数 的图像与函数 的图像交于点A,且点A的横坐标为2.
19. 已知(1)、化简T。(2)、若正方形ABCD的边长为a,且它的面积为9,求T的值。20. 随着移动互联网的快速发展,基于互联网的共享单车应运而生,为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.(1)、这组数据的中位数是 , 众数是 .(2)、计算这10位居民一周内使用共享单车的平均次数;(3)、若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数。21. 友谊商店A型号笔记本电脑的售价是a元/台,最近,该商店对A型号笔记本电脑举行促销活动,有两种优惠方案,方案一:每台按售价的九折销售,方案二:若购买不超过5台,每台按售价销售,若超过5台,超过的部分每台按售价的八折销售,某公司一次性从友谊商店购买A型号笔记本电脑x台。(1)、当x=8时,应选择哪种方案,该公司购买费用最少?最少费用是多少元?(2)、若该公司采用方案二方案更合算,求x的范围。22. 设P(x,0)是x轴上的一个动点,它与原点的距离为 。(1)、求 关于x的函数解析式,并画出这个函数的图象(2)、若反比例函数 的图像与函数 的图像交于点A,且点A的横坐标为2.①求k的值
②结合图像,当 时,写出x的取值范围。
23. 如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.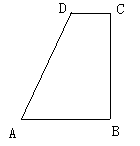 (1)、利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法)(2)、在(1)的条件下,
(1)、利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法)(2)、在(1)的条件下,①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值。
24. 已知抛物线 。(1)、证明:该抛物线与x轴总有两个不同的交点。(2)、设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在圆P上。①试判断:不论m取任何正数,圆P是否经过y轴上某个定点?若是,求出该定点的坐标,若不是,说明理由;
②若点C关于直线 的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为 ,圆P的半径记为 ,求 的值。
25. 如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC. (1)、求∠A+∠C的度数。(2)、连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由。(3)、若AB=1,点E在四边形ABCD内部运动,且满足 ,求点E运动路径的长度。
(1)、求∠A+∠C的度数。(2)、连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由。(3)、若AB=1,点E在四边形ABCD内部运动,且满足 ,求点E运动路径的长度。