四川省绵阳市2018年中考数学试卷
试卷更新日期:2018-06-20 类型:中考真卷
一、选择题
-
1. (-2018)0的值是( )A、-2018 B、2018 C、0 D、12. 四川省公布了2017年经济数据GDP排行榜,绵阳市排名全省第二,GDP总量为2075亿元。将2075亿元用科学记数法表示为( )A、 B、 C、 D、3. 如图,有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上。如果∠2=44°,那么∠1的度数是( )
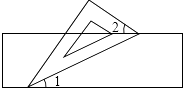 A、14° B、15° C、16° D、17°4. 下列运算正确的是( )A、 B、 C、 D、5. 下列图形中是中心对称图形的是( )
A、14° B、15° C、16° D、17°4. 下列运算正确的是( )A、 B、 C、 D、5. 下列图形中是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 6. 等式 成立的x的取值范围在数轴上可表示为( )A、
6. 等式 成立的x的取值范围在数轴上可表示为( )A、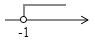 B、
B、 C、
C、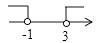 D、
D、 7. 在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )A、(4,-3) B、(-4,3) C、(-3,4) D、(-3,-4)8. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人9. 如图,蒙古包可近似看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25πm2 , 圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是( )
7. 在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )A、(4,-3) B、(-4,3) C、(-3,4) D、(-3,-4)8. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人9. 如图,蒙古包可近似看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25πm2 , 圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是( ) A、 B、40πm2 C、 D、55πm210. 一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据: )A、4.64海里 B、5.49海里 C、6.12海里 D、6.21海里11. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若AE= ,AD= ,则两个三角形重叠部分的面积为( )
A、 B、40πm2 C、 D、55πm210. 一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据: )A、4.64海里 B、5.49海里 C、6.12海里 D、6.21海里11. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若AE= ,AD= ,则两个三角形重叠部分的面积为( )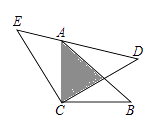 A、 B、 C、 D、12. 将全体正奇数排成一个三角形数阵
A、 B、 C、 D、12. 将全体正奇数排成一个三角形数阵1
3 5
7 9 11
13 15 17 19
21 23 25 27 29
… … … … … …
根据以上排列规律,数阵中第25行的第20个数是( )
A、639 B、637 C、635 D、633二、填空题
-
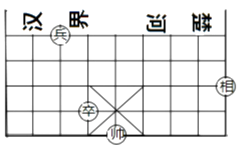
13. 因式分解: 。14. 如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,-1)和(-3,1),那么“卒”的坐标为。
 15. 现有长分别为1,2,3,4,5的木条各一根,从这5根木条中任取3根,能够构成三角形的概率是。16. 右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m。
15. 现有长分别为1,2,3,4,5的木条各一根,从这5根木条中任取3根,能够构成三角形的概率是。16. 右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m。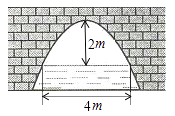 17. 已知a>b>0,且 ,则 。
17. 已知a>b>0,且 ,则 。
18. 如图,在△ABC中,AC=3,BC=4,若AC,BC边上的中线BE,AD垂直相交于点O,则AB=.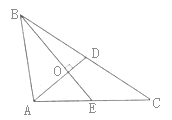
三、解答题。
-
19.(1)、计算:(2)、解分式方程:20. 绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:
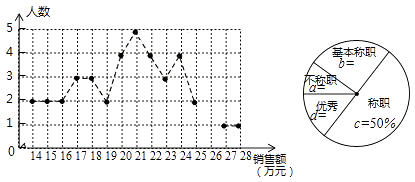
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当 时为“基本称职”,当 时为“称职”,当 时为“优秀”。根据以上信息,解答下列问题:
(1)、补全折线统计图和扇形统计图;(2)、求所有“称职”和“优秀”的销售员销售额的中位数和众数;(3)、为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一般人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由。21. 有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨。(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨?(2)、目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费话费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?22. 如图,一次函数 的图像与反比例函数 的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.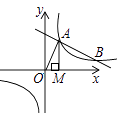 (1)、求反比例函数的解析式;(2)、在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标。23. 如图,AB是 的直径,点D在 上(点D不与A,B重合),直线AD交过点B的切线于点C,过点D作 的切线DE交BC于点E。
(1)、求反比例函数的解析式;(2)、在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标。23. 如图,AB是 的直径,点D在 上(点D不与A,B重合),直线AD交过点B的切线于点C,过点D作 的切线DE交BC于点E。 (1)、求证:BE=CE;(2)、若DE平行AB,求 的值。24. 如图,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(-3,0)。动点M,N同时从A点出发,M沿A→C,N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动时间记为t秒。连接MN。
(1)、求证:BE=CE;(2)、若DE平行AB,求 的值。24. 如图,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(-3,0)。动点M,N同时从A点出发,M沿A→C,N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动时间记为t秒。连接MN。 (1)、求直线BC的解析式;(2)、移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;(3)、当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式。25. 如图,已知抛物线 过点A 和B ,过点A作直线AC//x轴,交y轴与点C。
(1)、求直线BC的解析式;(2)、移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;(3)、当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式。25. 如图,已知抛物线 过点A 和B ,过点A作直线AC//x轴,交y轴与点C。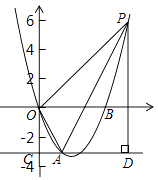 (1)、求抛物线的解析式;(2)、在抛物线上取一点P,过点P作直线AC的垂线,垂足为D,连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;(3)、抛物线上是否存在点Q,使得 ?若存在,求出点Q的坐标;若不存在,请说明理由。
(1)、求抛物线的解析式;(2)、在抛物线上取一点P,过点P作直线AC的垂线,垂足为D,连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;(3)、抛物线上是否存在点Q,使得 ?若存在,求出点Q的坐标;若不存在,请说明理由。